Das Optimierungsproblem
Das Volumen von Schachteln vergleichen
Wir betrachten weiterhin Schachteln, die aus einem DIN-A4-Blatt hergestellt werden, und vergleichen ihr Volumen.
Aufgabe 1
In einer Klasse wird über das Volumen der Schachteln diskutiert. Nimm dazu Stellung.
A. meint, dass alle Schachteln dasselbe Volumen haben müssten. Schließlich sind sie doch alle aus einem A4-Blatt erstellt.
B. stimmt zu: Je weiter man einschneidet, desto geringer wird zwar die Grundfläche, aber desto höher wird die Schachtel doch. Das Volumen muss gleich bleiben.
C. ist anderer Meinung: Je größer $x$ wird, desto mehr Papier wird abgeschnitten. Optimal ist also ein möglichst kleines $x$. Die Schachtel hat dann auch eine große Grundfläche.
Aufgabe 2 (optional)
(a) Trage erst einmal alle Daten zu den gebauten Schachteln in die Tabelle ein.
(b) Ergänze (evtl. arbeitsteilig) weitere Daten in der Tabelle. Zur Bestimmung der Volumina kannst du die Formel $V = (29.7 - 2x) \cdot (21 - 2x) \cdot x$ benutzen.
| x [Einschneidetiefe in cm] | V [Volumen in cm3] |
|---|---|
| ... | ... |
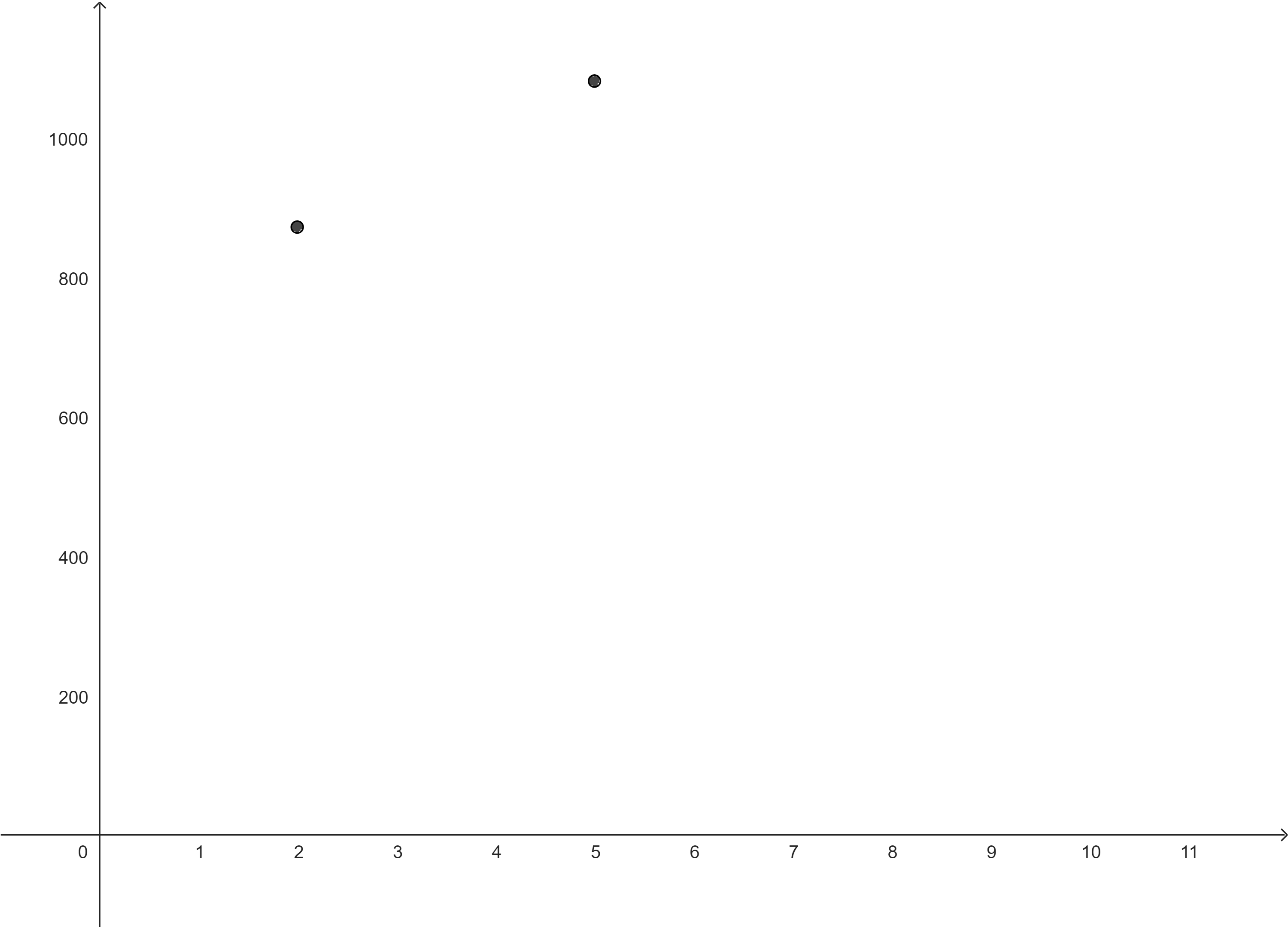
| 2 | 873.8 |
| ... | ... |
| 5 | 1083.5 |
| ... | ... |
(c)Trage die Werte in der Wertetabelle in ein Koordinatensystem ein.
Das Optimierungsproblem präzisieren
Die Wertetabelle und die zugehörige grafische Darstellung verdeutlichen sehr gut, dass Schachteln mit unterschiedlicher Einschneidetiefe sich (in aller Regel) in ihren Volumina unterscheiden. Es ergibt sich das folgende Optimierungsproblem.
Optimierungsproblem optimale Schachtel
Für welche Einschneidetiefe $x$ erhält man ein maximales Schachtelvolumen?
Aufgabe 3
Mit den Werten aus der Wertetabelle und der zugehörigen grafischen Darstellung kann man das Optimierungsproblem näherungsweise lösen. Schätze die optimale Einschneidetiefe mit diesen Werten ab.
Aufgabe 4
Das Optimierungsproblem lässt sich auch exakt lösen. Entwickle ein Strategie, wie man hier vorgehen könnte. Nutze die in den vorangehenden Kapiteln entwickelten Verfahren.
Wenn du fit bist, dann löse das Optimierungsproblem jetzt selbstständig. Nutze im Anschluss die nachfolgenden Seiten, um wichtige Fachbegriffe rund um Optimierungsprobleme kennenzulernen.
Wenn du weitere Hilfen benötigst, nutze direkt die folgenden Seiten.

