Zusammenfassung – 3D-Koordinatensysteme
Vereinbarungen
Wir haben festgestellt, dass es viele mathematisch richtige und sinnvolle Möglichkeiten gibt, wie man 3D-Koordinatensysteme zeichnen kann. Aber es wäre sehr kompliziert, wenn bei zehn Personen zehn verschiedene Möglichkeiten zum Einsatz kämen. So ließen sich Koordinatensysteme verschiedener Personen schlechter vergleichen. Deshalb müssen Vereinbarungen getroffen werden. Man nennt diese in der Mathematik Konventionen.
Koordinatensysteme für 3D-Darstellungen
Ein 3D-Koordinatensystem benutzt man, um die Position von Punkten im Raum mit Hilfe von Zahlen zu beschreiben. Ein 3D-Koordinatensystem ist analog zu einem 2D-Koordinatensystem aufgebaut: Es besteht also aus drei Achsen (Tiefe, Breite, Höhe), die im Raum zueinander senkrecht stehen und sich im Ursprung schneiden.
Die Lage eines Punktes kann man dann mithilfe eines Zahlentripels (Liste dreier Zahlen) darstellen.
Es gibt zahlreiche Möglichkeiten, 3D-Koordinatensysteme darzustellen, je nachdem, wie man die Achsen legt oder welche Hintergrundraster man benutzt. Hier drei Beispiele:
Variante 1:
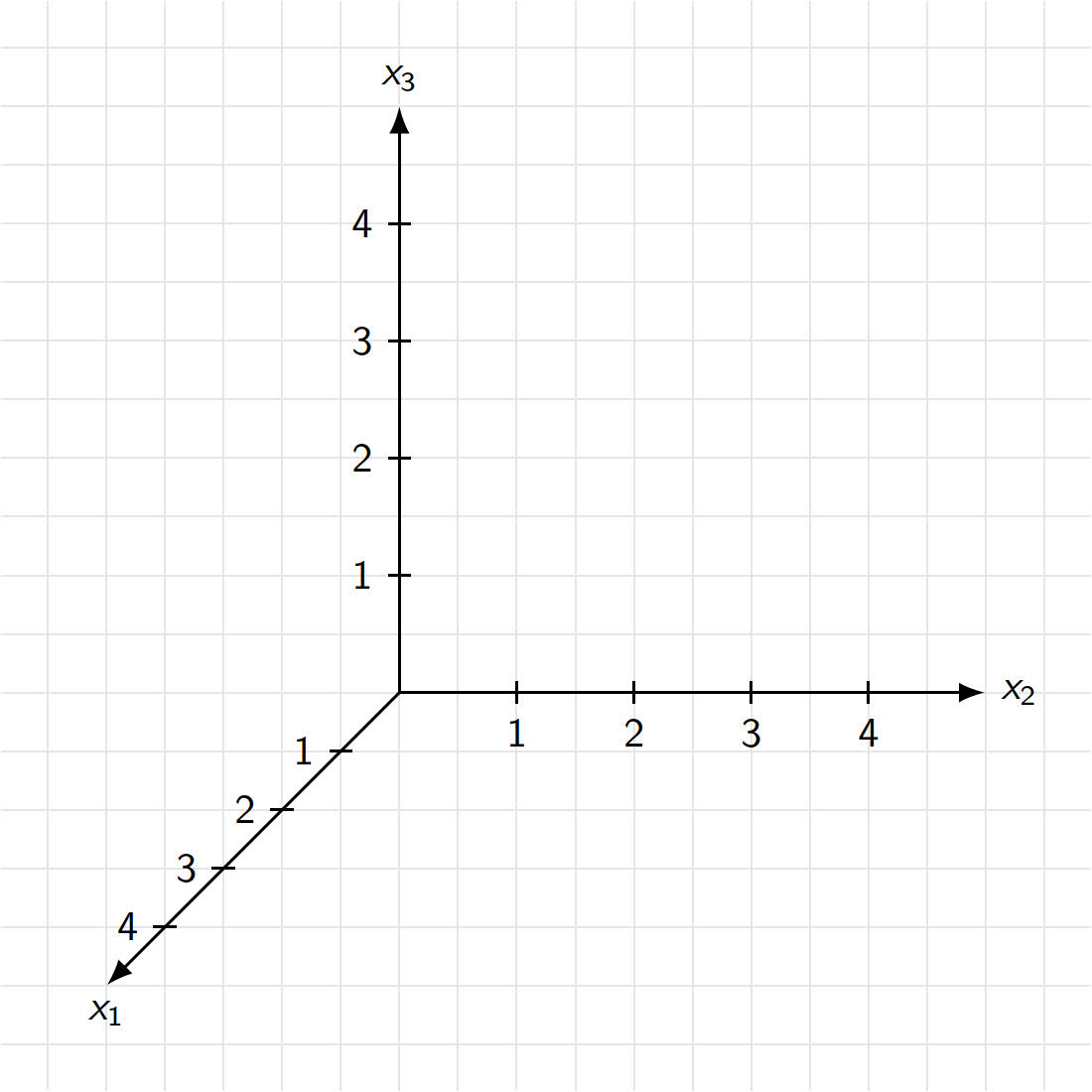
Variante 2:
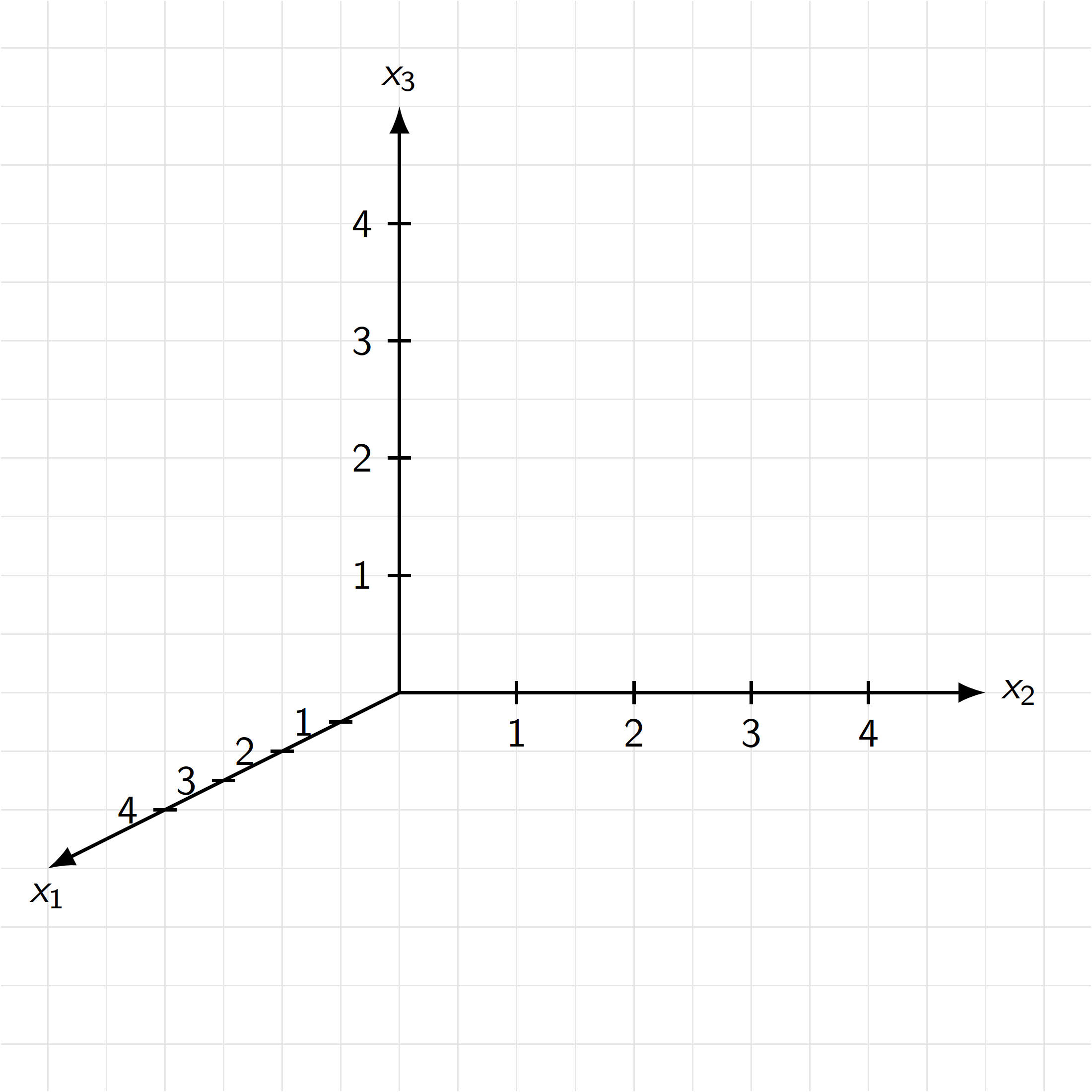
Variante 3 („isometrisch“):
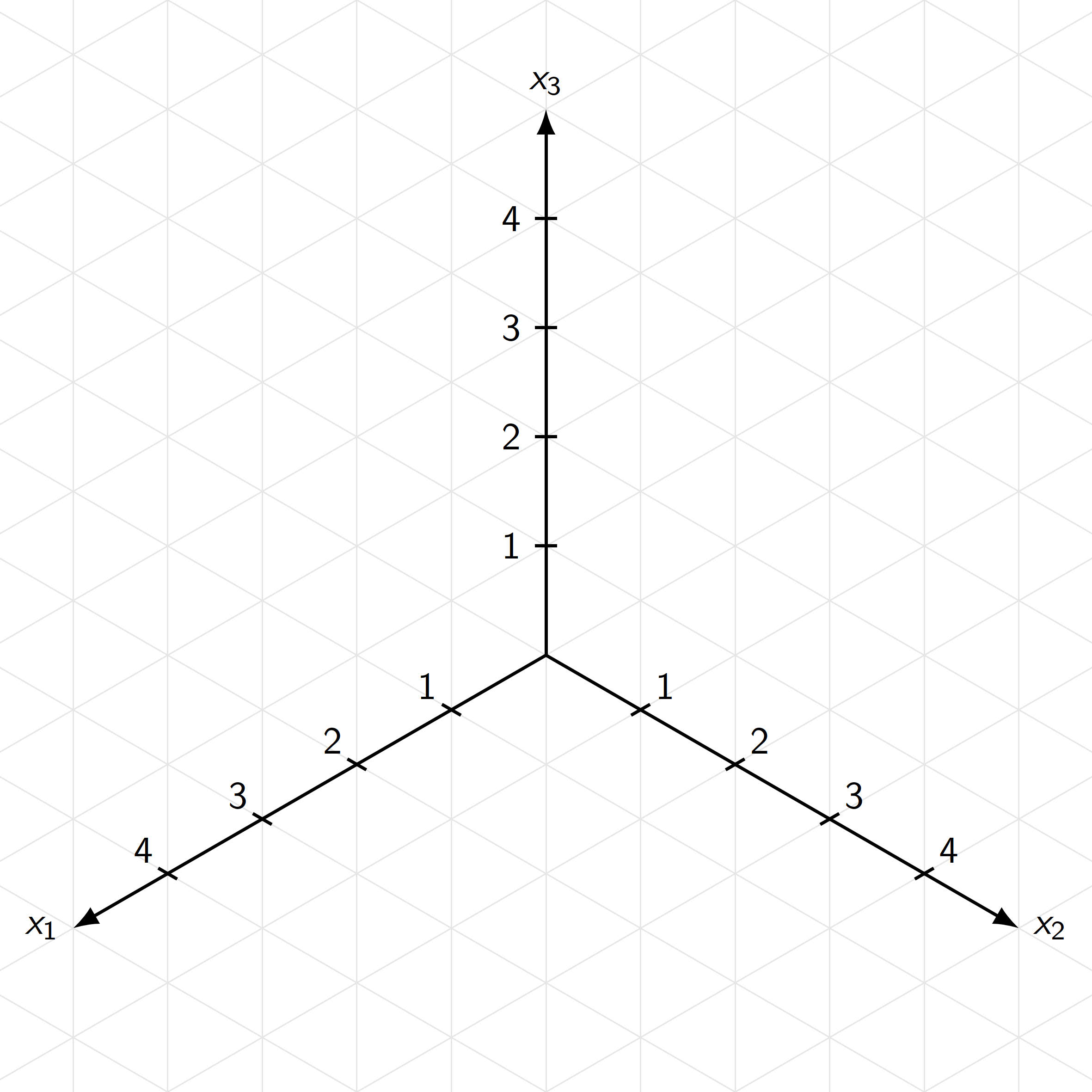
Wir werden in diesem Schulbuch Variante 1 verwenden.
Beachte:
- Die Achsen werden üblicherweise als $x_1$-Achse, $x_2$-Achse und $x_3$-Achse bezeichnet. Man benennt sie reihum gegen den Uhrzeigersinn.
- Die $x_1$-Achse wird oft so gezeichnet, dass sie nach vorne zeigt. Da es keine dritte Dimension auf dem Papier gibt, wird sie im 45°-Winkel dargestellt.
- Damit 3D-Objekte „richtig“ aussehen, wird die $x_1$-Achse verkürzt: Eine Einheit auf den anderen Achsen (also zwei Kästchen) entsprechen auf der $x_1$-Achse einer Kästchendiagnonale.
Punkte ins 3D-Koordinatensystem einzeichnen
Die folgende Abbildung zeigt, wie man Punkte mit vorgegebenen Koordinaten in ein 3D-Koordinatensystem einzeichnet.
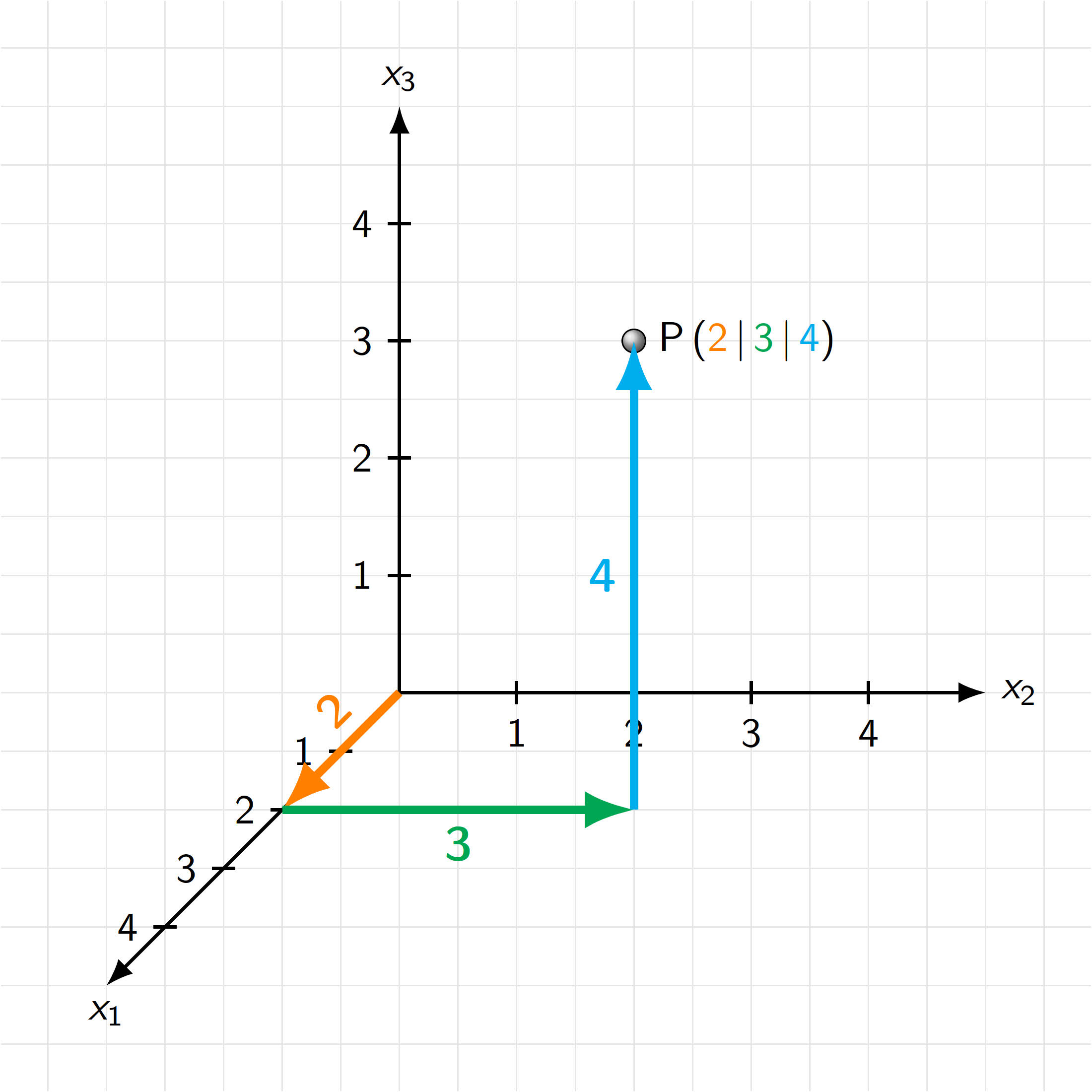
Punkte im 3D-Koordinatensystem ablesen
Achtung: In einem 3D-Koordinatensystem auf Papier kann man die Koordinaten eines Punktes nicht eindeutig ablesen.
Zum Herunterladen: punktBestimmenMitButton.ggb

