Zusammenfassung – Lineare Abhängigkeit von zwei Vektoren
Überprüfung auf Parallelität
Die Parallelität von zwei Stecken lässt sich mit Hilfe der entsprechenden Vektoren überprüfen.
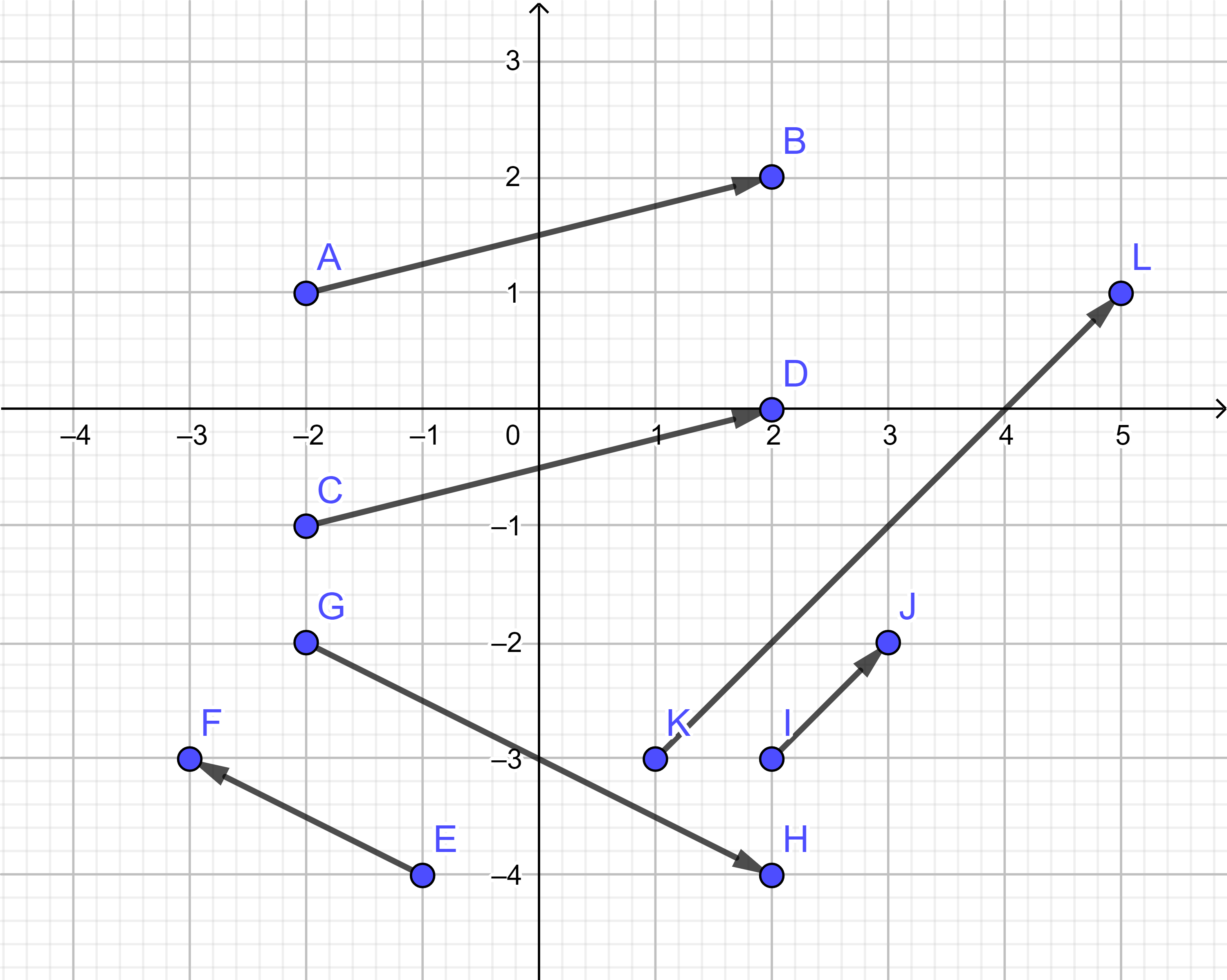
In der Abbildung sieht man, dass $\overrightarrow{ AB } = \overrightarrow{ CD }$. Die zugehörigen Seiten sind dann parallel.
Zusätzlich sieht man, dass $(-2) \cdot \overrightarrow{ EF } = \overrightarrow{ GH }$ bzw. $\overrightarrow{ EF } = (-0.5) \cdot \overrightarrow{ GH }$ sowie $4 \cdot \overrightarrow{ IJ } = \overrightarrow{ KL }$ bzw. $\overrightarrow{ IJ } = \frac{1}{4} \cdot \overrightarrow{ KL }$. Aus den Eigenschaften der skalaren Multiplikation kann man erschließen, dass die zugehörigen Seiten parallel sind.
Wenn ein Vektor ein skalares Vielfaches eines anderen Vektor ist, dann sind die zugehörigen Pfeile parallel. Umgekehrt gehören parallele Pfeile zu Vektoren, die skalare Vielfache voneinander sind.
Ein Fachbegriff für skalare Vielfache
Die Eigenschaft „skalares Vielfaches“ wird in der Mathematik mit einem Fachbegriff ausgezeichnet.
Definition:
Zwei Vektoren $\vec{u}$ und $\vec{v}$ nennt man linear abhängig genau dann, wenn es eine reelle Zahl $k$ gibt, sodass $\vec{u} = k\cdot \vec{v}$ oder $\vec{v} = k\cdot \vec{u}$. Wir schreiben dann $\vec{u} \parallel \vec{v}$.
Zwei Vektoren $\vec{u}$ und $\vec{v}$ nennt man linear unabhängig genau dann, wenn sie nicht linear abhängig sind.
Beispiele:
(a) Die Vektoren $\vec{u}= \left(\begin{array}{c} 2 \\ -1 \end{array}\right)$ und $\vec{v}= \left(\begin{array}{c} 4 \\ -2 \end{array}\right)$ sind linear abhängig, da $\vec{v} = 2 \cdot \vec{u}$ bzw. $\vec{u} = 0.5 \cdot \vec{v}$.
(b) Die Vektoren $\vec{u}= \left(\begin{array}{c} -4 \\ 0 \\ 8 \end{array}\right)$ und $\vec{v}= \left(\begin{array}{c} 1 \\ 0 \\ -2 \end{array}\right)$ sind linear abhängig, da $\vec{u}= (-4) \cdot \vec{v}$ bzw. $\vec{v} = (-\frac{1}{4}) \cdot \vec{u}$.
(c) Die Vektoren $\vec{u}= \left(\begin{array}{c} 1 \\ 1 \\ 2 \end{array}\right)$ und $\vec{v}= \left(\begin{array}{c} 2 \\ 2 \\ 6 \end{array}\right)$ sind nicht linear abhängig, da keiner der beiden Vektoren ein Vielfaches des anderen ist.
Sonderfall – Nullvektor
Wenn einer der beiden Vektoren der Nullvektor ist, dann sind die beiden Vektoren auf jeden Fall linear abhängig.
Die Vektoren $\vec{u}= \left(\begin{array}{c} -7 \\ 13 \end{array}\right)$ und $\vec{v}= \left(\begin{array}{c} 0 \\ 0 \end{array}\right)$ sind linear abhängig, da $\vec{b}= 0 \cdot \vec{a}$.
Beachte, dass im vorliegenden Beispiel $\vec{v}= \left(\begin{array}{c} 0 \\ 0 \end{array}\right)$ ein Vielfaches von $\vec{u}= \left(\begin{array}{c} -7 \\ 13 \end{array}\right)$ ist. $\vec{u}= \left(\begin{array}{c} -7 \\ 13 \end{array}\right)$ ist aber kein Vielfaches von $\vec{v}= \left(\begin{array}{c} 0 \\ 0 \end{array}\right)$.
Regelfall – kein Nullvektor
Wenn keiner der beiden Vektoren der Nullvektor ist, dann gilt:
Wenn Vektor $\vec{u}$ ein Vielfaches von $\vec{v}$ ist (d.h. $\vec{u} = k \cdot \vec{v}$ mit einer reellen Zahl $k$), dann ist auch umgekehrt $\vec{v}$ ein Vielfaches von $\vec{u}$ (da $\frac{1}{k} \cdot \vec{u} = \vec{v}$).
Beispiel: Für die Vektoren $\vec{u}= \left(\begin{array}{c} -4 \\ 0 \\ 8 \end{array}\right)$ und $\vec{v}= \left(\begin{array}{c} 1 \\ 0 \\ -2 \end{array}\right)$ gilt: $\vec{u}= (-4) \cdot \vec{v}$ und somit $(-\frac{1}{4}) \cdot \vec{u} = \vec{v}$.
Wenn keiner der beiden Vektoren $\vec{u}$ und $\vec{v}$ der Nullvektor ist, dann reicht es, folgende Bedingung zu überprüfen: Gibt es eine reelle Zahl $k$, so dass Vektor $\vec{u} = k \cdot \vec{v}$ gilt.
Überprüfung auf lineare Abhängigkeit bei zwei Vektoren
Beispiel 1:
Sind $\vec{u}= \left(\begin{array}{c} 3 \\ 4 \\ -2 \end{array}\right)$ und $\vec{v}= \left(\begin{array}{c} 1.2 \\ 1.6 \\ -0.8 \end{array}\right)$ linear abhängig?
Lösung
Bedingung: $\vec{u} = k \cdot \vec{v}$ bzw. $\left(\begin{array}{c} 3 \\ 4 \\ -2 \end{array}\right) = k \cdot \left(\begin{array}{c} 1.2 \\ 1.6 \\ -0.8 \end{array}\right)$ bzw. $\left(\begin{array}{c} 3 \\ 4 \\ -2 \end{array}\right) = \left(\begin{array}{c} k \cdot 1.2 \\ k \cdot 1.6 \\ k \cdot (-0.8) \end{array}\right)$
Hieraus ergibt sich das folgende lineare Gleichungssystem (LGS):
$\begin{array}{lrcrcrcr} [1] &\quad 3 & = & 1.2k \\ [2] &\quad 4 & = & 1.6k \\ [3] &\quad -2 & = & -0.8k \end{array}$
Auflösen von [1] ergibt: $k = 2.5$
Auflösen von [2] ergibt: $k = 2.5$
Auflösen von [3] ergibt: $k = 2.5$
Es gibt also eine reelle Zahl $k$ (hier: 2.5), so dass $\vec{u} = k \cdot \vec{v}$ gilt. Die beiden Vektoren sind folglich linear abhängig.
Beispiel 2:
Sind $\vec{u}= \left(\begin{array}{c} 4 \\ 4 \\ -2 \end{array}\right)$ und $\vec{v}= \left(\begin{array}{c} -1.6 \\ -1.6 \\ 1 \end{array}\right)$ linear abhängig?
Lösung
Bedingung: $\vec{u} = k \cdot \vec{v}$ bzw. $\left(\begin{array}{c} 4 \\ 4 \\ -2 \end{array}\right) = k \cdot \left(\begin{array}{c} -1.6 \\ -1.6 \\ 1 \end{array}\right)$ bzw. $\left(\begin{array}{c} 4 \\ 4 \\ -2 \end{array}\right) = \left(\begin{array}{c} k \cdot (-1.6) \\ k \cdot (-1.6) \\ k \cdot 1 \end{array}\right)$
Hieraus ergibt sich das folgende lineare Gleichungssystem (LGS):
$\begin{array}{lrcrcrcr} [1] &\quad 4 & = & -1.6k \\ [2] &\quad 4 & = & -1.6k \\ [3] &\quad -2 & = & k \end{array}$
Auflösen von [1] ergibt: $k = -2.5$
Auflösen von [2] ergibt: $k = -2.5$
Auflösen von [3] ergibt: $k = -2$
Es gibt also keine reelle Zahl $k$, so dass $\vec{u} = k \cdot \vec{v}$ gilt. Die beiden Vektoren sind folglich nicht linear abhängig.

