Ausblick

Anwendung im Game Design

Kommen wir nochmal zurück zur Anwendung im Game Design. Hier sind gegebenenfalls noch zwei Fragen offen:

1. Warum haben wir bisher nur Dreiecke und keine komplizierten Figuren betrachtet?
2. Benötigt man dort wirklich Vektoren? Wie arbeitet der Computer mit den Figuren?

Zu Frage 1: Komplizierte Figuren

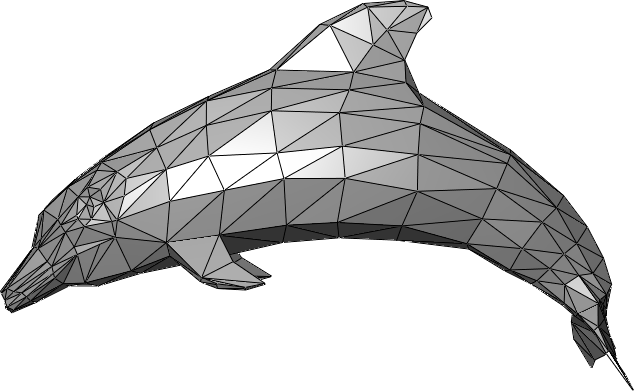
Verschiebungen (und auch andere Bewegungen wie Drehungen etc.) lassen sich für Punkte mithilfe von Vektoren berechnen. Ein komplizierter (ggf. auch dreidimensionaler) Körper wird in der Computergrafik deshalb durch ein Netz von einfachen Vielecken angenähert. Oft nutzt man Dreiecksnetze („triangle mesh“); dieses Thema wird erneut auf der Seite zur Flächenbeschreibung im Kontext von Ebenen angesprochen.

Man kann nun die Eckpunkte der Dreiecke beliebig verschieben/drehen und bewegt so auch den gesamten Delphin.

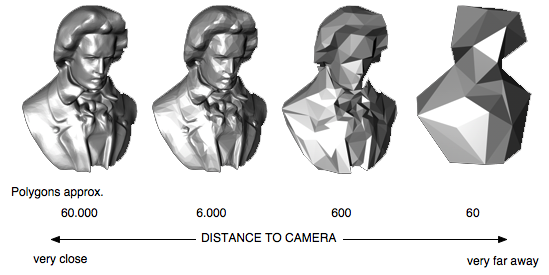
Je mehr Dreiecke man nutzt, desto weniger erkennt man diese Annäherung.

Zu Frage 2: Mathematik am Computer

Eine gerechtfertigte Frage ist natürlich, ob wir uns diesen Kontext nur ausgedacht haben, um Vektoren irgendwie „schmackhaft zu machen“, oder ob man beim Game Design wirklich Vektoren nutzt.

Die Antwort dazu ist ganz einfach: Eine kurze Youtube-Suche nach „Mathe Game Design“ fördert eine Playlist zu Tage: „Math for Game Developers“ umfasst über 100 Videos. Gleich das erste beschäftigt sich mit Vektoren, um Objekte zu verschieben.

In den Videos geht es dann auch darum, wie man mit solchen Vektoren rechnet. Genau das werden wir uns im nächsten Unterkapitel ansehen.