Erkundung – Geocaching

Schatzsuche

Geocaching ist eine moderne Form der Schatzsuche. Ein Geocache (das ist ein Behälter mit einem kleinen Schatz) wird von einem Anbieter an einem interessanten Ort (z.B. in einem Wald unter einem markanten Stein) abgelegt. Die geografischen Koordinaten dieses Ortes werden dann von dem Anbieter im Internet veröffentlicht. Jeder Nutzer kann dann mit den Koordinateninformationen auf die Suche nach dem Schatz gehen. Damit die Schatzsuche herausfordernder wird, werden die Koordinateninformationen oft in Form eines Rätsels dargeboten.

Wir spielen Teile dieser Schatzsuche in vereinfachter Form jetzt mit einer Karte von Kaiserslautern [1] durch.

Aufgabe 1 (Einstieg)

(a) „Der Schatz befindet sich genau in der Mitte zwischen der Tropfsteinhöhle und dem Humberg.“ Markiere grob die Lage des Schatzes in der Karte unterhalb der Aufgabe.

(b) Beschreibe, wie man das Problem geometrisch mit Zirkel und Lineal lösen kann. Kontrolliere deine Lösungsidee, indem du auf „Geometrische Lösung“ klickst.

(c) In der Realität ist dieses Vorgehen nicht so einfach möglich. Erläutere die Schwierigkeiten.

(d) In der Praxis nutzt man beim Geocaching GPS-Koordinaten zur Bestimmung der Lage. Wir wollen dieselbe Idee verfolgen. Beschreibe, was wir tun müssen, um dieses Problem mithilfe von Koordinaten zu lösen.

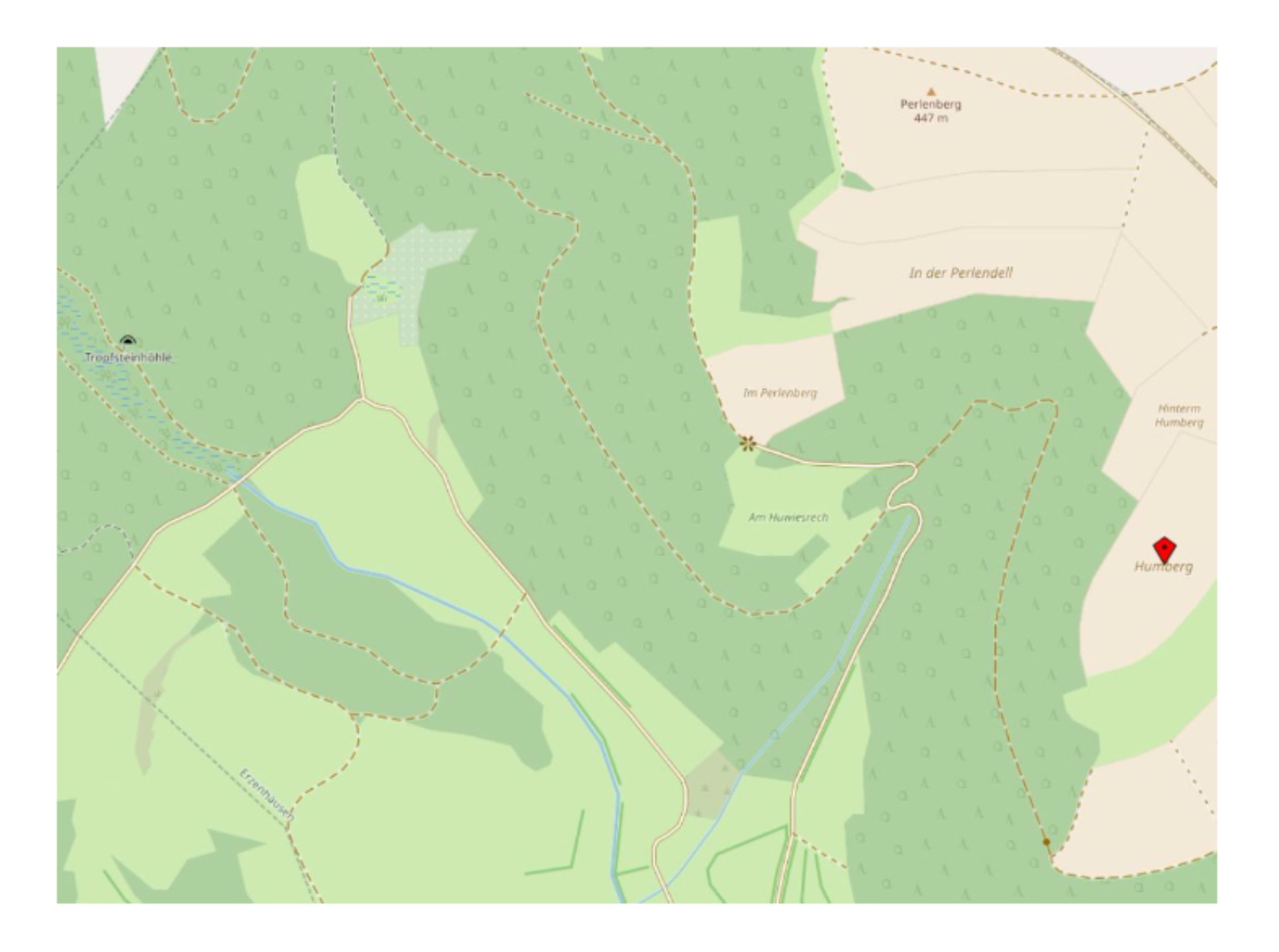
1. Problemstellung
2. Geometrische Lösung

Klicke auf die einzelnen Schritte zur Veranschaulichung.

🎯 Leitfrage

Wie bestimmen wir die Position des Schatzes in der Mitte der Tropfsteinhöhle und des Humbergs mit Koordinaten?

Das Versteck mit Hilfe von Koordinaten ermitteln

Aufgabe 2 (Erarbeitung)

(a) Die Koordinaten der beiden Ausgangspunkte sind im Applet unterhalb der Aufgabe eingetragen: Die Höhle liegt bei $A(-5|4)$ und der Turm bei $B(9|1)$. Bestimme die Koordinaten des Mittelpunkts $M$ durch Ablesen.

(b) Wie hätte man die Koordinaten des Mittelpunkts $M$ auch direkt aus den Koordinaten der beiden Ausgangspunkte $A(-5|4)$ und $B(9|1)$ erschließen können? Erläutere kurz.

(c) Du kannst die Lage der beiden Ausgangspunkte $A$ und $B$ variieren, indem du die Punkte im Koordinatensystem bewegst. Das Applet ist so eingestellt, dass sich immer ganzzahlige Koordinaten ergeben. Entwickle ein Verfahren, mit dem man die Koordinaten von $M$ direkt aus den Koordinaten von $A$ und $B$ berechnen kann. Überprüfe das Verfahren mit verschiedenen Beispielen.

Zum Herunterladen: mittelpunkt2.ggb

Hinweis zur Darstellung von Punkten

Wenn du GeoGebra nicht im Schulbuch, sondern separat öffnest, dann steht neben einem Punkt $A$ eventuell nicht $A(-5|4)$, sondern $A=(-5,4)$. Das ist eine andere mögliche Schreibweise zur Beschriftung von Punkten. Wir nutzen in o-mathe die – in deutschen Schulen verbreitete – Schreibweise mit dem „|“ zwischen den beiden Koordinaten und ohne „=“ zwischen Punkt und Klammer.

Vorgaben dazu, wie etwas in der Mathematik aufgeschrieben wird, nennt man eine Notation. Wir nutzen also die $A(a_1|a_2)$-Notation zur Darstellung von Punkten.

Aufgabe 3 (Sicherung)

(a) 🖊️ Beschreibe das Verfahren zur Mittelpunktsberechnung möglichst präzise in Worten.

(b) 🖊️ In der Mathematik nutzt man Formeln, um ein Rechenverfahren möglichst kurz zu beschreiben. Vervollständige den folgenden Satz:

„Wenn der Punkt $A$ die Koordinaten $A(a_1|a_2)$ und $B$ die Koordinaten $B(b_1|b_2)$ hat, dann kann man die Koordinaten von $M(m_1|m_2)$ so berechnen: ...“

(c) 🚀 Das hier entwickelte Verfahren lässt sich auch in der Praxis anwenden. Recherchiere, wie man mit GPS-Koordinaten vorgeht.

Rückschau auf das Vorgehen: Analytische Geometrie

Aufgabe 4 (Vertiefung)

(a) Wir haben nun für ein geometrisches Problem zwei Lösungswege gefunden: Auf der einen Seite geometrisch mit Zirkel und Lineal und auf der anderen Seite rechnerisch (man sagt auch „algebraisch“). Ordne im nachfolgenden Schaubild zu, wie wir vorgegangen sind.

(b) 💬 Erkläre das Schaubild deinem Sitznachbarn.

(c) Sammle Vor- und Nachteile des algebraischen Vorgehens.

Ausblick

Die Welt, in der wir leben, ist dreidimensional. Das haben wir bisher noch nicht berücksichtigt. In den weiteren Kapiteln werden wir das bearbeitete Problem nochmal aufgreifen, dann aber in 3D. Hierzu müssen wir erst einmal 3D-Koordinatensysteme einführen.