Strukturierung
Differenzen und Summen bestimmen
Aufgabe 1
Der Laserschweißer hat bereits ein Parallelogramm entlang der blauen Vektoren geschweißt. Nun sollen noch die Diagonalen folgen:
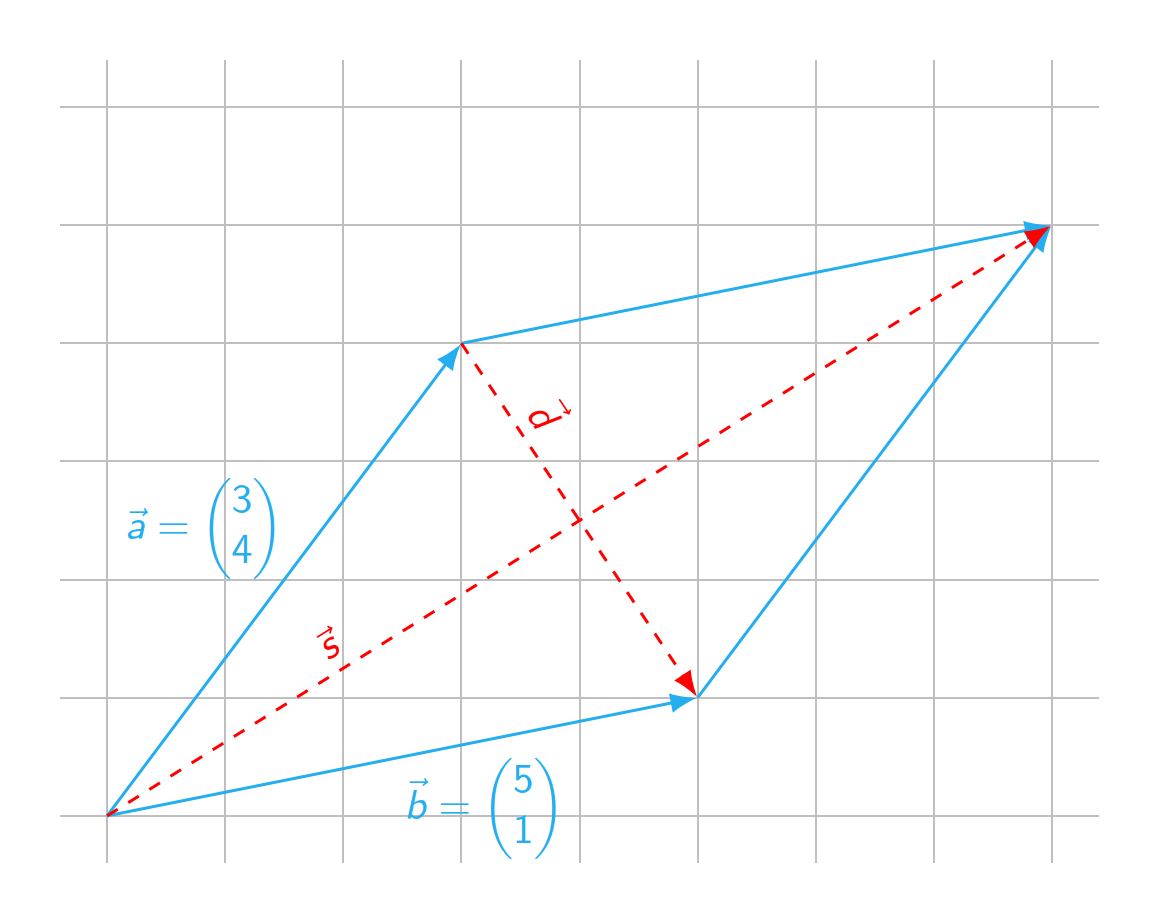
(a) Ermittle die Einträge der Vektoren $\vec{s}$ und $\vec{d}$, die die roten Nähte beschreiben. Achte genau auf die Orientierung der Vektoren.
(b) Einen der roten Vektoren könnte man als Summe der beiden blauen Vektoren bezeichnen, den anderen als deren Differenz. Begründe diese beiden Aussagen.
(c) Vervollständige die folgenden Sätze:
Vektoraddition und -subtraktion:
- Zwei Vektoren werden rechnerisch addiert, indem man ...
Anschaulich bedeutet die Addition, dass die Pfeile ... - Zwei Vektoren werden rechnerisch subtrahiert, indem man ...
Anschaulich bedeutet die Subtraktion, dass ...
Aufgabe 2
(a) Zeichne in den ersten beiden Fällen jeweils die Vektoren auf Karopapier und ermittle zeichnerisch die Ergebnisvektoren. Ermittle die Ergebnisvektoren in allen drei Fällen rechnerisch.
- $\begin{pmatrix} 3 \\ 4 \end{pmatrix} + \begin{pmatrix} 2 \\ 3 \end{pmatrix}$
- $\begin{pmatrix} 4 \\ -2 \end{pmatrix} - \begin{pmatrix} 3 \\ 0 \end{pmatrix}$
- $\begin{pmatrix} 1 \\ 5 \\ 2 \end{pmatrix} + \begin{pmatrix} -3 \\ 4 \\ -2 \end{pmatrix}$
(b) Der Nullvektor $\begin{pmatrix} 0 \\ 0 \end{pmatrix}$ bzw. $\begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}$ ist ein besonderer Vektor. Erkläre an Beispielen, was damit gemeint ist.
(c) Bei Zahlen sagt man, dass $-2$ die Gegenzahl von $2$ ist; $5$ ist die Gegenzahl von $-5$. Beschreibe, wie man für einen Vektor $\vec{a}$ rechnerisch den Gegenvektor $-\vec{a}$ erhält und wie die beiden geometrisch zusammen hängen?
(d) Überlege, welche Fehler beim Addieren und – vor allem – beim Subtrahieren auftreten könnten.
Die Verwandtschaft zwischen Differenz und Summe beschreiben
Aufgabe 3
Jan behauptet, die Vektoraddition und Vektorsubtraktion seien miteinander verwandt. Dazu hat er die folgende Skizze erstellt.
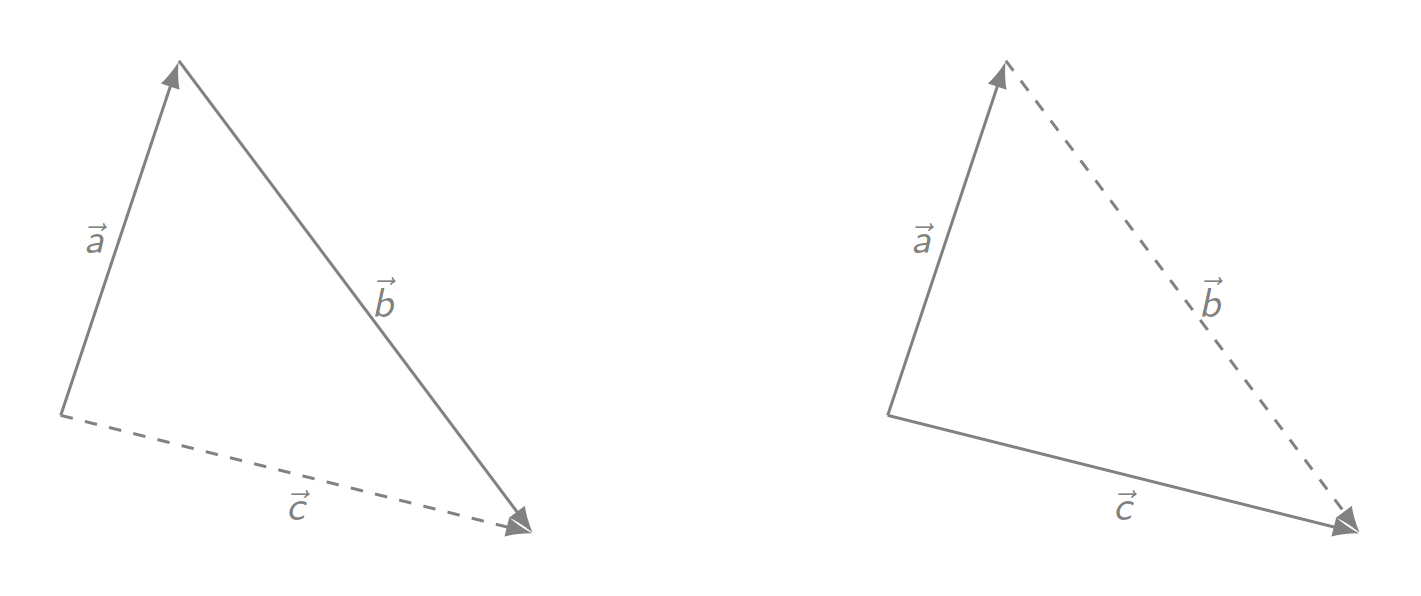
Erkläre, was Jan mit seiner Aussage meint.
💡 Hinweis
Vielleicht hilft der Vergleich zur Addition und Subtraktion von Zahlen: Die Rechnungen $3+7 = 10$ und $10-7 = 3$ hängen ja auch miteinander zusammen.
Die Subtraktion auf Kommutativität untersuchen
Aufgabe 4
„Es ist ein Unterschied, ob man $\vec{a}-\vec{b}$ rechnet oder $\vec{b}-\vec{a}$.“ – Belege diese Aussage mit einem Beispiel. Untersuche, worin sich die beiden Ergebnisvektoren unterscheiden und gleichen.
🚀 Es gibt Sonderfälle, in denen es keinen Unterschied macht. Gib solche Fälle an.
Das erworbene Wissen im Wissensspeicher zusammenfassen
Aufgabe 5
🖊️ Trage dein bislang erworbenes Wissen in den Wissensspeicher ein.
