Erkundung – Längenberechnung

Abstände und Längen in Computerspielen

Julia spielt ein Computerspiel, in dem sie eine kleine Drohne steuert und Diamanten einsammelt. Die Drohne verbraucht beim Flug Energie; sammelt sie einen Diamanten auf, wird die Energie wieder aufgeladen.

Beim Spielen bekommt Julia die folgende Fehlermeldung:

Aufgabe 1 (Einstieg)

(a) Erkläre kurz die Fehlermeldung.

(b) Kennst du weitere Computerspiele, in denen Entfernungen oder die Länge von Bewegungen eine Rolle spielen?

🎯 Leitfrage

Wie können wir (in Computerspielen) Entfernungen von Punkten oder die Länge von Bewegungen berechnen?

Aufgabe 2 (Erarbeitung)

(a) 👤👤 Suche dir eine:n Partner:in. Im Applet unter der Aufgabe könnt ihr selbst eine Drohne steuern. Versucht, vom Punkt $H(2|3)$ ausgehend von Diamant zu Diamant zu fliegen. Aber Achtung: Jede einzelne Flugstrecke darf nur 5 Einheiten lang sein. Wer schafft es, mehr Diamanten einzusammeln? Notiert euch eure verwendeten Vektoren sowie die Punkte, die ihr erreicht.

(b) Auf den ersten Blick kann man nicht für alle Strecken, die die Drohne fliegt, die Länge genau ablesen. Vielleicht wart ihr euch sogar uneinig, ob manche Strecken erlaubt sind. Blende das Lineal ein und miss aus, wie lang die einzelnen Strecken/Vektoren sind.

(c) Julia hat die Drohne von Diamant $B$ zu Diamant $C$ fliegen lassen, also entlang des Vektors $\begin{pmatrix}4\\1\end{pmatrix}$. Sie meint: Die Drohne geht vier Schritte nach rechts und einen nach oben; die Strecke ist genau 5 lang – also gerade noch erlaubt.“ Miss nach. Erkläre, wo Julias Denkfehler liegt. Nutze ggf. das Hilfs-Dreieck.

Zum Herunterladen: diamanten-sammler-2d.ggb

Anleitung für das Applet

Drücke auf den Button „Drohne startklar machen“. Jetzt kannst du die Bewegungsdaten (rot, oben links) verändern. Drücke nun auf „Drohne fliegen lassen“; die Drohne fliegt zum neuen Punkt $P'$. Drücke nun auf „Neue Drohnenposition anzeigen“ und in der Grafik oben werden die Koordinaten von $P'$ angezeigt.

Nun kannst du erneut auf „Drohne startklar machen“ klicken. Danach ist $P$ auf der Position des vorherigen $P'$ und du kannst die Drohne von hier aus weiter steuern.

Aufgabe 3 (Sicherung)

(a) Vergleicht eure Ergebnisse: Hat jede:r dieselben Flugstrecken ausgewählt? Welche Möglichkeiten gibt es?

(b) In Aufgabe 2 habt ihr einen Weg festgestellt, die Länge einer Flugstrecke bzw. den Abstand von Punkten zu bestimmen. Bestimme für die Diamanten-Punkte $A(-3|2)$, $B(2|-1)$, $C(6|0)$ und $D(9|4)$ den Abstand vom Drohnen-Landeplatz $H(2|3)$ rechnerisch.

💡 Tipp

Nutze das Hilfs-Dreieck im Applet und den Satz des Pythagoras.

Was sagt nochmal der Satz des Pythagoras aus?

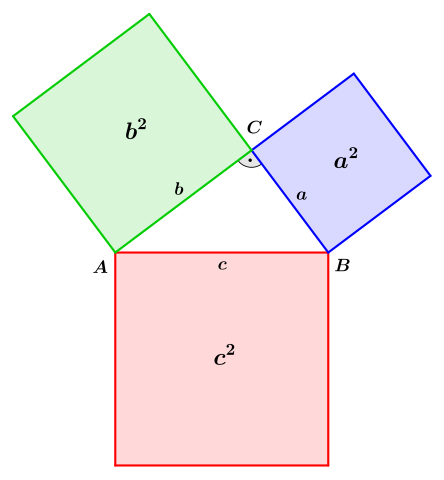
Der Satz des Pythagoras besagt: In einem rechtwinkligen Dreieck gilt: Wenn $a$ und $b$ die Längen der Kathetenseiten sind und $c$ die Länge der Hypotenuse (das ist die Seite gegenüber dem rechten Winkel), dann gilt $a^2 + b^2 = c^2$.

[1]

Mit dem Satz des Pythagoras kann man auch Seitenlängen im rechtwinkligen Dreieck berechnen: Falls nötig, stelle die Gleichung $a^2+b^2=c^2$ nach der gesuchten Seite um und ziehe dann die Wurzel.

(c) 🖊️ Verallgemeinere im Heft:

💡 Tipp

Betrachte für den zweiten Teil den Drohnenflug/Vektor $\overrightarrow{ AB }$.

Aufgabe 4 (Vertiefung)

Julia hat das nächste Level erreicht und steuert ihre Drohne nun durch den dreidimensionalen Raum.

(a) Julias Zeit läuft ab; sie muss noch schnell vom Ursprung $O$ aus zum nächsten Diamant. Drei Edelsteine sind erkennbar: $A$, $B$ und $C$. Lies die Koordinaten im Applet unter der Aufgabe ab und bestimme die Abstände der Diamanten zum Ursprung. Welcher Diamant ist am nächsten am Ursprung?

💡 Hilfestellung

Am einfachsten ist der Drohnenflug $\overrightarrow{ OC }$, weil er nur in eine Richtung geht. Der Drohnenflug $\overrightarrow{ OB }$ funktioniert wie in Aufgabe 2. Der Drohnenflug $\overrightarrow{ OA }$ geht aber in alle drei Richtungen. Dafür müssen wir noch etwas mehr nachdenken.

Hier siehst du den relevanten Ausschnitt des Koordinatensystems vergrößert.

Zum Herunterladen: betragvektor1.ggb

Weitere Hilfe

Wir interessieren uns für die Länge des roten Pfeils. Der ist Teil des roten Dreiecks. Weil das Dreieck rechtwinklig ist, können wir mit dem Satz des Pythagoras die gesuchte Seite ausrechnen, wenn wir die anderen beiden Seiten kennen. Leider kennen wir aber nur eine von beiden.

Die fehlende Seite im roten Dreieck ist aber auch Teil des blauen Dreiecks. Darin kennen wir zwei von den drei Seiten. Nutze also zweimal den Satz des Pythagoras, um die Länge des roten Pfeils zu bestimmen.

(b) Julia hat sich zum nächsten Diamant gerettet. Ein paar Sekunden hat sie noch, bevor die Runde endet. Welcher der beiden Punkte liegt näher an ihrer aktuellen Position?

Zum Herunterladen: diamanten-sammler-3d.ggb

(c) 🖊️ Verallgemeinere im Heft: