Übungen – 3D-Koordinaten
Körper in Koordinatensystemen zeichnen
Du kannst hoffentlich bereits 3D-Koordinatensysteme zeichnen und Punkte darin eintragen. Nun geht es darum, kompliziertere Körper zusammenzusetzen – auf Papier und am Rechner. Das ist für die analytische Geometrie notwendig, damit du dir die kommenden Themen skizzieren und vorstellen kannst.
Aufgabe 1 – Ein 3D-Puzzle ★
Wenn man die 7 Puzzle-Teile passend zusammensetzt, erhält man einen Würfel.
vorher:
nachher:
Die Puzzleteile sollen mit einem 3D-Drucker erstellt werden. Hierzu müssen die einzelnen Puzzleteile erst einmal genau beschrieben werden. Ziel der Aufgabe ist es, diese Beschreibung mit Hilfe geeigneter Punkte in einem 3D-Koordinatensystem zu erstellen.
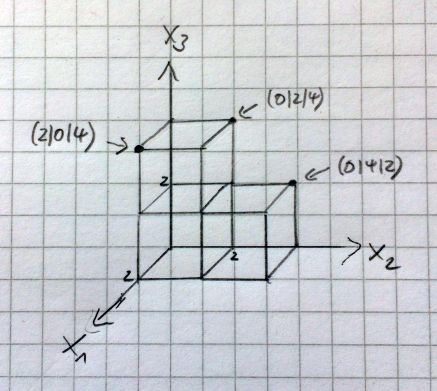
(a) Betrachte das folgende Puzzleteil. Dieses Puzzleteil ist aus 3 Würfeleinheiten zusammengesetzt. Wir gehen davon aus, dass die einzelnen Würfel zwei Längeneinheiten lang, breit und hoch sind. Erstelle eine Skizze zu diesem Puzzleteil und bestimme die Koordinaten aller Eckpunkte des Puzzleteils.
💡 Skizze mit manchen Koordinaten
Einige Koordinaten müssen noch bestimmt werden.
(b) Benutze das GeoGebra-Applet, um die Koordinaten zu überprüfen. Gib die Koordinaten der Eckpunkte im GeoGebra-Eingabefenster ein, z.B. so: „$A=(0,0,0)$“ Du siehst direkt, ob sie stimmen.
Zum Herunterladen: Puzzle2.ggb
(c) Gehe bei den anderen drei Puzzleteilen analog vor. Positioniere das Puzzleteil in geeigneter Weise im Koordinatensystem. Erstelle jeweils eine Skizze mit den Koordinaten der Eckpunkte. Überprüfe sie anschließend mit Hilfe von GeoGebra.
(d) 🚀 Zum Weiterdenken: Jedes Puzzleteil besteht aus einer bestimmten Anzahl von Würfeln. Ermittle die Gesamtanzahl aller Würfel, aus denen die Puzzleteile bestehen. Begründe, dass man aus so vielen kleinen Würfeln einen großen Würfel bauen kann.
(e) 🚀 Zum Experimentieren: Wenn du die Möglichkeit hast, die Puzzleteile selbst herzustellen, dann probiere selbst aus, wie man die Puzzleteile zu einem Würfel zusammensetzen kann.
Aufgabe 2 – Gebäude zeichnen
In dieser Aufgabe geht es darum, sich ein 3-dimensionales Gebilde vorzustellen und (im Kopf) die Koordinaten wichtiger Punkte zu bestimmen.
(a) ★ Die folgende Abbildung zeigt ein Haus mit Walmdach.
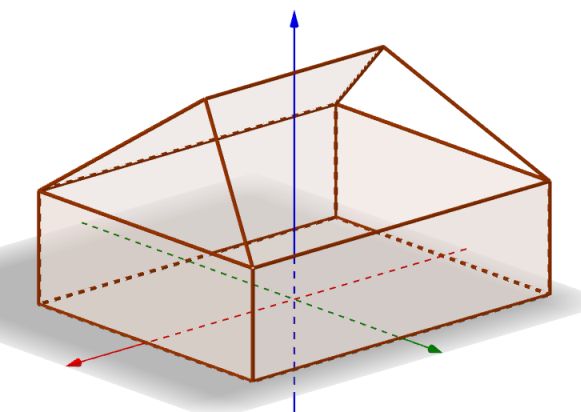
Gehe von folgenden Ausmaßen aus:
- Länge: 10 LE
- Breite: 8 LE
- Höhe des Erdgeschosses: 3 LE
- Gesamthöhe mit Dach: 6 LE
- Länge der oberen Dachkante: 6 LE
Bestimme alle Eckpunkte des Hauses und fertige eine exakte 3D-Skizze des Hauses an. Du kannst deine Lösung mit dem Applet unterhalb der Aufgabe kontrollieren.
(b) ★★★ Die Liebfrauenkirche in Trier zählt zu den bedeutendsten gotischen Zentralbauten in Deutschland.
Betrachte einen Gebäudekomplex, dessen Form sich an der Liebfrauenkirche in Trier orientiert:
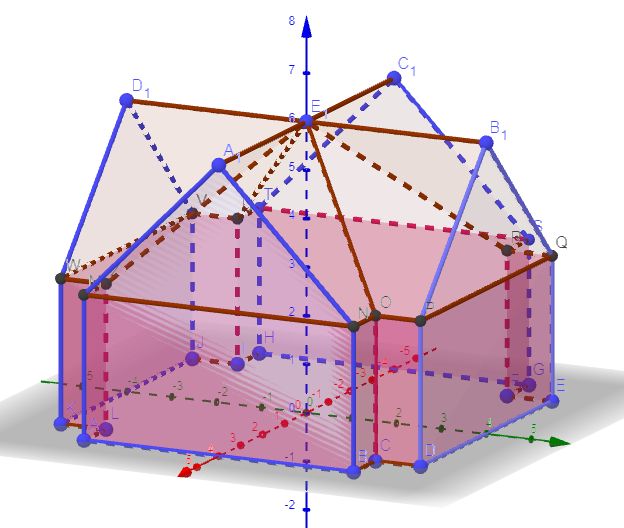
Lege selbst die Ausmaße fest und konstruiere das Gebäude mit GeoGebra. Dabei musst du alle relevanten Eckpunkte des Gebäudes bestimmen.
In diesem Applet kannst du Punkte z.B. so eingeben: „$A=(0,0,0)$“
Zum Herunterladen: gebaeude.ggb
Aufgabe 3 – 3D-Mittelpunktsberechnung ★★
Im letzten Unterkapitel wurde gezeigt, wie man den Mittelpunkt einer Strecke in der 2D-Ebene rechnerisch bestimmen kann. Hier geht es darum, das Verfahren auf Strecken im 3D-Raum zu übertragen.
Wie bestimmt man rechnerisch den Mittelpunkt $M$ der Strecke $\overline{AB}$, wenn man die Koordinaten von $A$ und $B$ kennt?
(a) Die Koordinaten der beiden Punkte $A$ und $B$ sind im Applet unterhalb der Aufgabe voreingestellt. Bestimme rechnerisch die Koordinaten des Mittelpunkts $M$ der Strecke $\overline{AB}$. Überprüfe, indem du den Punkt im Eingabefenster eingibst (z.B. so: „$M=(0,0,0)$“) und dann schaust, ob er auch tatsächlich an der gewünschten Stelle liegt.
(b) Variiere jetzt die Lage von $A$ und $B$, indem du die Punkte im Koordinatensystem bewegst. Bestimme jeweils die Koordinaten des Mittelpunkts $M$ und überprüfe seine Lage.
Zum Herunterladen: mittelpunkt3d.ggb
Probleme beim Ablesen von Punkten
Du hast schon in den vorangegangenen Abschnitten Probleme beim Ablesen von Punkten in 3D-Koordinatensystemen festgestellt. Das soll in der nachfolgenden Aufgabe weiter vertieft werden.
Aufgabe 4 – Punkte im Koordinatensystem ablesen ★★
Gegeben ist ein Punkt $P$ in einer 2D-Darstellung eines 3D-Koordinatensystems (siehe Abbildung). Welche Koordinaten hat der Punkt $P$?
(a) A. behauptet: „Klar, sieht man doch: $P(0|2|2)$“. B. entgegnet: „Ganz so klar ist das nicht.“ Setze die Argumentation von B. fort. Bestimme weitere Möglichkeiten für die Koordinaten des Punktes $P$, die zur Abbildung passen.
Hier kannst du es selbst ausprobieren.
Zum Herunterladen: punkt3D2ggb
(b) Kann $P$ auch die Koordinaten $P(10|6|8)$ haben? Bestimme zunächst systematisch die Punkte mit den Koordinaten $P(1|...|...)$, $P(2|...|...)$, $P(3|...|...)$ usw., die alle zur Abbildung passen. Kläre anschließend die Frage.
(c) Kann $P$ auch die Koordinaten $P(-10|-3|-3)$ haben? Gehe zur Klärung der Frage analog zu (b) vor.
Quellen
- [1]: Liebfrauenkirche in Trier - Urheber: Soloneying - Lizenz: Creative Commons BY-SA 4.0
