Zusammenfassung – Betrag eines Vektors
Länge von Vektorpfeilen
In vielen Anwendungssituationen kann man Abstände berechnen, indem man die Länge geeigneter Vektorpfeile bestimmt. Für die Länge von Vektorpfeilen wird daher ein neuer Begriff eingeführt.
Unter dem Betrag eines Vektors versteht man die Länge der zugehörigen Vektorpfeile.
Man schreibt $\left| \vec{v} \right|$ für den Betrag von $\vec{v}$.
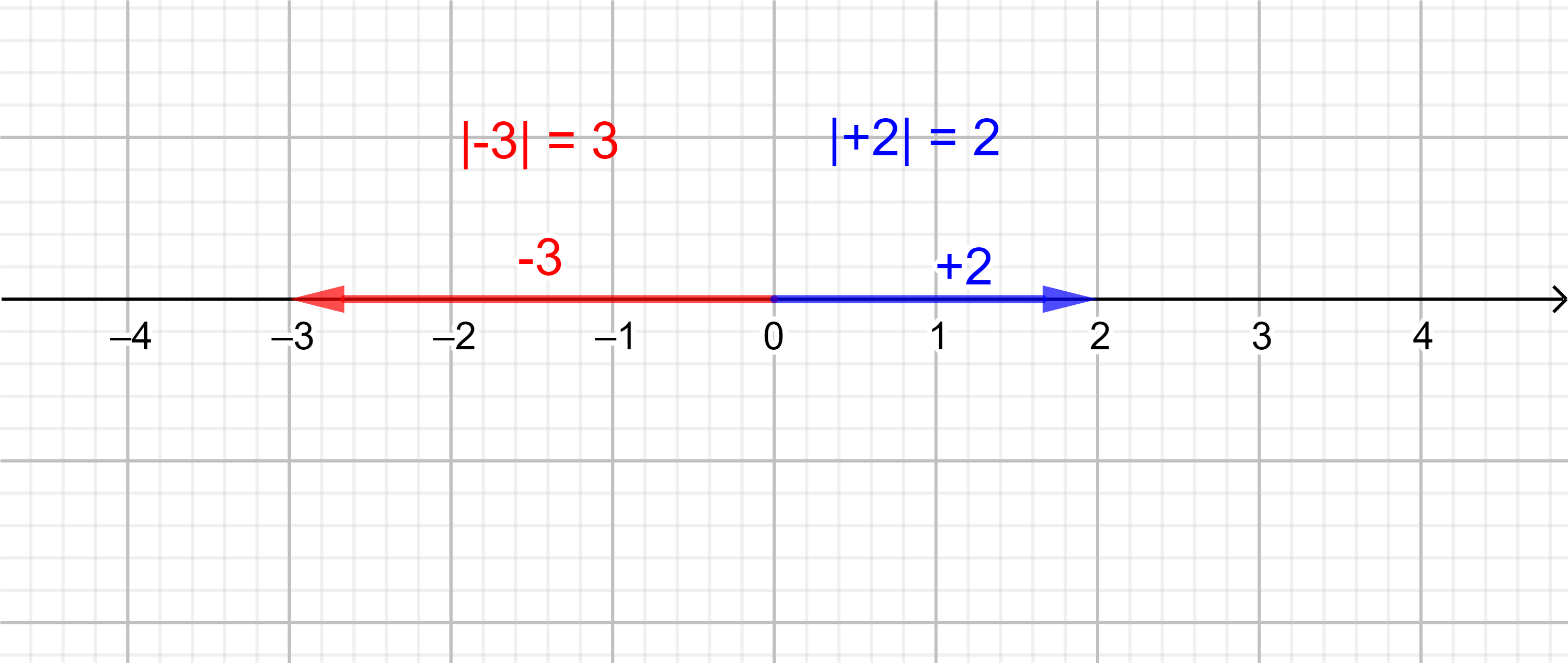
Man nutzt für die Länge von Vektoren also denselben Begriff und dieselbe Schreibweise wie beim Betrag von Zahlen. Auch die dahintersteckende Grundidee ist analog: Mit dem Betrag von Zahlen beschreibt man den Abstand von Koordinatenursprung bzw. die Länge des Pfeils vom Koordinatenursprung zur betreffenden Zahl auf der Zahlengeraden.
Betrag eines Vektors – 2D-Fall
Gegeben ist der Vektor $\vec{v}$ mit den Koordinaten $\vec{v} = \left(\begin{array}{c} v_1 \\ v_2 \end{array}\right)$.
Gesucht ist eine Formel zur Berechnung des Betrags $|\vec{v}|$, den wir hier kurz mit $v$ beschreiben.
Zum Herunterladen: betrag2D.ggb
Der Betrag eines Vektors $\vec{v} = \left(\begin{array}{c} v_1 \\ v_2 \end{array}\right)$ lässt sich mit der folgenden Formel berechnen: $|\vec{v}| = \sqrt {v_1^2 + v_2^2}$.
Herleitung
Der Vektor $\vec{v}$ legt ein (blau dargestelltes) Dreieck PTQ fest, das bei T einen rechten Winkel hat (siehe Applet).
Nach dem Satz des Pythagoras gilt für das blau dargestellte Dreieck: $v^2 = v_1^2 + v_2^2$.
Durch Wurzelziehen erhält man jetzt $v = \sqrt {v_1^2 + v_2^2}$.
Beispiel:
Für $\vec{v} = \left(\begin{array}{c} 2 \\ -4 \end{array}\right)$ erhält man $|\vec{v}| = \sqrt {2^2 + (-4)^2} = \sqrt{20} \approx 4.47$.
Betrag eines Vektors – 3D-Fall
Gegeben ist der Vektor $\vec{v}$ mit den Koordinaten $\vec{v} = \left(\begin{array}{c} v_1 \\ v_2 \\ v_3 \end{array}\right)$.
Gesucht ist eine Formel zur Berechnung des Betrags $|\vec{v}|$, den wir hier kurz mit $v$ beschreiben.
Zum Herunterladen: betrag3D.ggb
Der Betrag eines Vektors $\vec{v} = \left(\begin{array}{c} v_1 \\ v_2 \\ v_3 \end{array}\right)$ lässt sich mit der folgenden Formel berechnen: $|\vec{v}| = \sqrt {v_1^2 + v_2^2 + v_3^2}$.
Herleitung
Der Vektor $\vec{v}$ legt ein (blau dargestelltes) Dreieck PTQ fest, das bei T einen rechten Winkel hat (siehe Applet).
Im Applet ist zusätzlich das (rot dargestellte) Dreieck PST hervorgehoben, das bei S einen rechten Winkel hat.
Nach dem Satz des Pythagoras gilt für das rot dargestellte Dreieck: $h^2 = v_1^2 + v_2^2$.
Nach dem Satz des Pythagoras gilt für das blau dargestellte Dreieck: $v^2 = h^2 + v_3^2$.
Setzt man das Ergebnis für $h^2$ aus der ersten Gleichung in die zweite Gleichung für $v^2$ ein, so erhält man $v^2 = v_1^2 + v_2^2 + v_3^2$.
Durch Wurzelziehen erhält man jetzt $v = \sqrt {v_1^2 + v_2^2 + v_3^2}$.
Beispiel:
Für $\vec{v} = \left(\begin{array}{c} 1 \\ -4 \\ -2 \end{array}\right)$ erhält man $|\vec{v}| = \sqrt {1^2 + (-4)^2 + (-2)^2} = \sqrt{21} \approx 4.58$.
Abstandsberechnung mit Hilfe von Vektoren
Der Abstand $d(P, Q)$ der beiden Punkte $P(1|2)$ und $Q(8|-1)$ soll bestimmt werden.
Lösung
Zum Herunterladen: abstand2D.ggb
Zunächst bestimmt man den Vektor $\overrightarrow{ PQ } = \left(\begin{array}{c} 7 \\ -3 \end{array}\right)$.
Den gesuchten Abstand erhält man dann so: $d(P, Q) = | \overrightarrow{ PQ } | = \sqrt{7^2 + (-3)^2} = \sqrt{58} \approx 7.62$.

