Strukturierung – Betrag eines Vektors
Die Länge von Vektorpfeilen bestimmen
In der Erkundung hast du gelernt, wie man die Länge von Drohnenflügen, die durch Vektoren beschrieben werden, ausrechnen kann. Damit hast du in 2D und 3D den Abstand von Punkten berechnet.
Die Länge von Vektoren ist wichtig genug, dass sie einen eigenen Fachbegriff erhält:
Unter dem Betrag eines Vektors versteht man die Länge der zugehörigen Vektorpfeile.
Man schreibt $\left| \vec{v} \right|$ für den Betrag von $\vec{v}$.
Aufgabe 1 (Einstieg & Vernetzung)
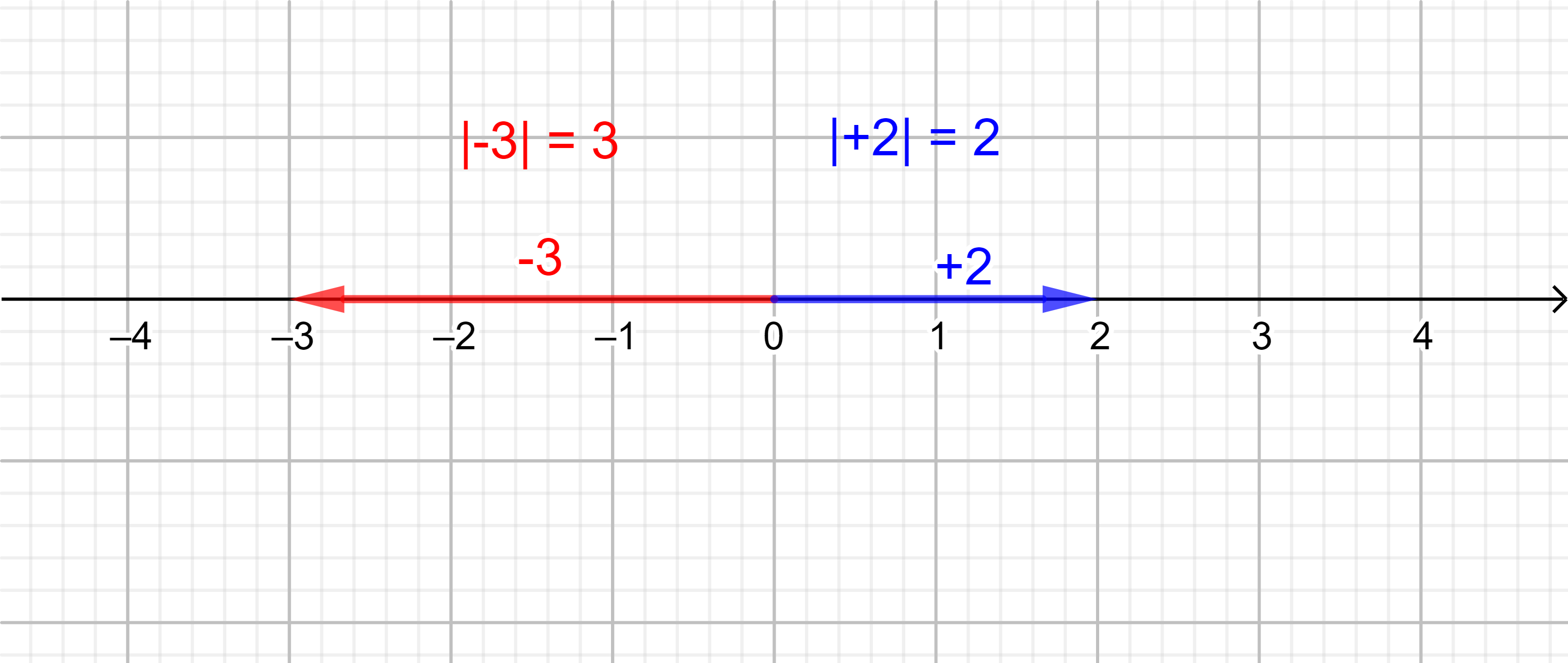
Den Begriff Betrag kennst du bereits von Zahlen. Beschreibe den Zusammenhang mithilfe des folgenden Bilds:
Tipp
Versuche, Zahlen als Vektoren in einer Dimension, also auf der Zahlengerade, zu begreifen.
Formel für den Betrag
Du hast auch schon herausgefunden, wie man Beträge berechnet:
Der Betrag eines Vektors $\vec{v} = \left(\begin{array}{c} v_1 \\ v_2 \end{array}\right)$ lässt sich mit der folgenden Formel berechnen: $|\vec{v}| = \sqrt {v_1^2 + v_2^2}$.
Der Betrag eines Vektors $\vec{v} = \left(\begin{array}{c} v_1 \\ v_2\\v_3 \end{array}\right)$ lässt sich mit der folgenden Formel berechnen: $|\vec{v}| = \sqrt {v_1^2 + v_2^2+v_3^2}$.
Aufgabe 2 (Einstieg & Wiederholung)
Erkläre die Formeln mithilfe des folgenden Applets. Du siehst darin den roten Vektorpfeil $\vec{v}$ als Ortsvektor des Punktes $V$. Wenn du $V$ verschiebst, ändert sich auch der Vektor mitsamt den Hilfsdreiecken.
Zum Herunterladen: betragvektor1.ggb
Eigenschaften des Betrages
Der Betrag von Zahlen erfüllt einige Eigenschaften:
- Nicht-Negativität: Für alle reelle Zahlen $x$ gilt: $|x| \geq 0$.
- Zusammenhang von Zahl und Gegenzahl: Für alle reelle Zahlen $x$ gilt: $|x| = |-x|$.
- „Dreiecksungleichung“: Für alle reelle Zahlen $x$ und $y$ gilt: $|x+y| \le |x| + |y|$.
Aufgabe 3 (Erarbeitung)
Gelten die Aussagen über den Betrag von Zahlen auch für den Betrag von Vektoren? Nutze das folgende Applet, um das zu überprüfen. Teste dabei auch, wie mit negativen Koordinaten umgegangen wird.
Zum Herunterladen: betragvektor1.ggb
Aufgabe 4 (Vertiefung) 🚀
Da man mit Beträgen Abstände zwischen Punkten bestimmen kann, hängen die Eigenschaften von Beträgen eng mit den Eigenschaften von Abständen zusammen.
(a) Begründe mit Abstandsargumenten oder mithilfe der Eigenschaften von Vektoren, dass die folgenden Zusammenhänge plausibel sind.
- Für alle Punkte $A$ gilt: $ \left| \overrightarrow{ AA } \right| = 0$.
- Für alle Punkte $A$ und $B$ gilt: $ \left| \overrightarrow{ AB } \right| = \left| \overrightarrow{ BA } \right|$.
- Für alle Punkte $A$, $B$ und $C$ gilt: $ \left| \overrightarrow{ AB } \right| + \left| \overrightarrow{ BC } \right| \geq \left| \overrightarrow{ AC } \right|$.
(b) Überprüfe die aufgelisteten Eigenschaften exemplarisch mit jeweils selbst gewählten Punkten.
(c) Für welche Konstellationen der Punkte $A$, $B$ und $C$ gilt: $ \left| \overrightarrow{ AB } \right| + \left| \overrightarrow{ BC } \right| = \left| \overrightarrow{ AC } \right|$? Überprüfe mit selbst gewählten Punkten.
Das Wichtigste notieren
Du hast nun die wichtigsten Eigenschaften des Betrags kennengelernt. Zeit, das festzuhalten.
Aufgabe 5 (Sicherung)
✏️️ Halte das Gelernte in diesem Wissensspeicher fest.

