Zusammenfassung – Vektorbegriff
Vektor als Zahlentupel – die algebraische Sicht
Im vorangegangenen Abschnitt haben wir Zahlentupel benutzt, um Bewegungen in der 2D-Ebene und im 3D-Raum zu beschreiben. Solche Zahlentupel spielen eine zentrale Rolle in der Analytischen Geometrie und werden daher mit einem neuen Begriff ausgezeichnet.
Definition: Vektor
Ein Vektor ist ein Tupel aus 2 bzw. 3 (allgemein $n$) reellen Zahlen. Die Zahlen, aus denen ein Vektor besteht, werden Koordinaten des Vektors genannt.
Beispiel: Zahlenpaare bzw. Tupel mit 2 Zahlen
$\vec{a}= \left(\begin{array}{c} 2 \\ -1 \end{array}\right)$, $\vec{b}= \left(\begin{array}{c} 4 \\ 0.5 \end{array}\right)$, $\vec{c}= \left(\begin{array}{c} 0 \\ 0 \end{array}\right)$, ..., $\vec{v}= \left(\begin{array}{c} v_1 \\ v_2 \end{array}\right)$
Beispiel: Zahlentripel bzw. Tupel mit 3 Zahlen
$\vec{a}= \left(\begin{array}{c} 1 \\ -1 \\ 4 \end{array}\right)$, $\vec{b}= \left(\begin{array}{c} 6.1 \\ 0.1 \\ -2.5 \end{array}\right)$, $\vec{c}= \left(\begin{array}{c} 0 \\ 0 \\ 0 \end{array}\right)$, ..., $\vec{v}= \left(\begin{array}{c} v_1 \\ v_2 \\ v_3 \end{array}\right)$
Variablen zur Bezeichnung von Vektoren werden – wie in den Beispielen gezeigt – mit einem Vektorpfeil versehen. Das ist eine in der Schule verbreitete Konvention; außerhalb der Schule gibt es auch andere Konventionen.
Vektor als Verschiebung – eine geometrische Deutung
Vektoren kann man benutzen, um Verschiebungen (bzw. Bewegungen) in der Ebene und im Raum zu beschreiben.
Eine Verschiebung ist eine Abbildung, die jedem Punkt der 2D-Ebene (bzw. des 3D-Raums) einen Bildpunkt zuordnet. Die Zuordnung wird dabei durch einen Verschiebungspfeil festgelegt.
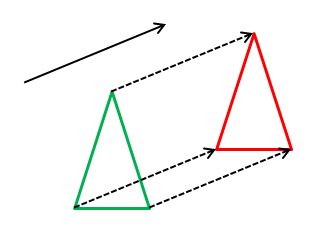
Wenn ein Koordinatensystem gegeben ist, dann kann man einen Verschiebungspfeil mit einem Zahlentupel eindeutig beschreiben.
Vektor als Verschiebung – 2D-Fall
Zum Herunterladen: vektoren2D4.ggb
Betrachte das Beispiel im Applet.
Der Vektor $\left(\begin{array}{c} 6 \\ 3 \end{array}\right)$ bewirkt folgende Verschiebung:
- $6$ in $x_1$-Richtung (bzw. $x$-Richtung)
- $3$ in $x_2$-Richtung (bzw. $y$-Richtung)
Der Vektor $\left(\begin{array}{c} 6 \\ 3 \end{array}\right)$ führt also z.B. zu den folgenden Abbildungen:
- $A(-4|2) \rightarrow A'(2|1)$
- $B(-2|-3) \rightarrow B'(4|0)$
- $C(-3|1) \rightarrow C'(3|4)$
Vektor als Verschiebung – 3D-Fall
Zum Herunterladen: vektoren3D3a.ggb
Betrachte das Beispiel im Applet.
Der Vektor $\left(\begin{array}{c} -2 \\ 3 \\ 1 \end{array}\right)$ bewirkt folgende Verschiebung:
- $-2$ in $x_1$-Richtung
- $3$ in $x_2$-Richtung
- $1$ in $x_3$-Richtung
Der Vektor $\left(\begin{array}{c} -2 \\ 3 \\ 1 \end{array}\right)$ führt also z.B. zu den folgenden Abbildungen:
- $A(3|-1|2) \rightarrow A'(1|2|3)$
- $B(2|-1|1) \rightarrow B'(0|2|2)$
Vektoren werden üblicherweise in einer Grafik mit Vektorpfeilen dargestellt. Ein Vektor kann – wie im Beispiel oben – durch mehrere (sogar unendlich viele) Pfeile dargestellt werden.
Die Pfeildarstellung spiegelt sich auch in der folgenden Schreibweise wider:
$\overrightarrow{ AA' } = \left(\begin{array}{c} -2 \\ 3 \\ 1 \end{array}\right)$ und $\overrightarrow{ BB' } = \left(\begin{array}{c} -2 \\ 3 \\ 1 \end{array}\right)$
Ortsvektoren
Ortsvektoren dienen dazu, die Lage von Punkten im Koordinatensystem mit Vektoren zu beschreiben.
Zum Herunterladen: ortsvektor.ggb
Hier wird der Vektor $\vec{p} = \overrightarrow{ OP }$ benutzt, um die Lage des Punktes $P$ zu beschreiben. Beide - Punkt und zugehöriger Ortsvektor - haben dieselben Koordinaten.
Definition Ortsvektor
Der Ortsvektor zu einem Punkt $P$ ist der Vektor $\overrightarrow{ OP }$ vom Koordinatenursprung $O$ zum Punkt $P$.
Schreibweise:
Der Ortsvektor $\overrightarrow{ OP }$ zum Punkt $P$ wird meist mit $\vec{p}$ bezeichnet. Man verwendet hier also den entsprechenden Kleinbuchstaben.
Beispiel:
Der Ortsvektor zum Punkt $P(4|1)$ ist der Vektor $\overrightarrow{ OP } = \left(\begin{array}{c} 4 \\ 1 \end{array}\right)$ vom Koordinatenursprung $O$ zum Punkt $P$.
Bestimmung von Vektoren
Wenn die Koordinaten von Anfangs- und Endpunkt eines Vektorpfeils gegeben sind, dann lässt sich aus diesen Koordinaten direkt der zugehörige Vektor bestimmen.
Satz:
Aus $A(a_1 | a_2 | a_3 )$ und $B(b_1 | b_2 | b_3 )$ erhält man den Verbindungsvektor $\overrightarrow{ AB } = \left(\begin{array}{c} b_1 - a_1 \\ b_2 - a_2 \\ b_3 - a_3 \end{array}\right)$
Beispiel:
Aus $A(7 | 0 | -1 )$ und $B(5 | 3 | -2 )$ erhält man $\overrightarrow{ AB } = \left(\begin{array}{c} 5-7 \\ 3-0 \\ -2-(-1) \end{array}\right) = \left(\begin{array}{c} -2 \\ 3 \\ -1 \end{array}\right)$

