Zusammenfassung
Die Addition und Subtraktion eines Vektors kann man graphisch mit Pfeilen und rechnerisch mit n-Tupeln deuten:
Addition zweier Vektoren
Wenn man sagt, dass man zwei Vektoren $\vec{a}=\begin{pmatrix}a_1\\a_2\\a_3\end{pmatrix}$ und $\vec{b}=\begin{pmatrix}b_1\\b_2\\b_3\end{pmatrix}$ addiert, meint man damit, dass man deren einzelne Komponenten addiert: $$\vec{a}+\vec{b}=\begin{pmatrix}a_1\\a_2\\a_3\end{pmatrix}+\begin{pmatrix}b_1\\b_2\\b_3\end{pmatrix}=\begin{pmatrix}a_1+b_1\\a_2+b_2\\a_3+b_3\end{pmatrix}.$$
Graphisch bedeutet die Addition zweier Vektoren $\vec{a}=\begin{pmatrix}a_1\\a_2\\a_3\end{pmatrix}$ und $\vec{b}=\begin{pmatrix}b_1\\b_2\\b_3\end{pmatrix}$, dass deren Pfeile zu einem Gesamtpfeil (resultierender Vektor, Summenvektor) zusammengefügt werden, der den direkten Weg angibt:
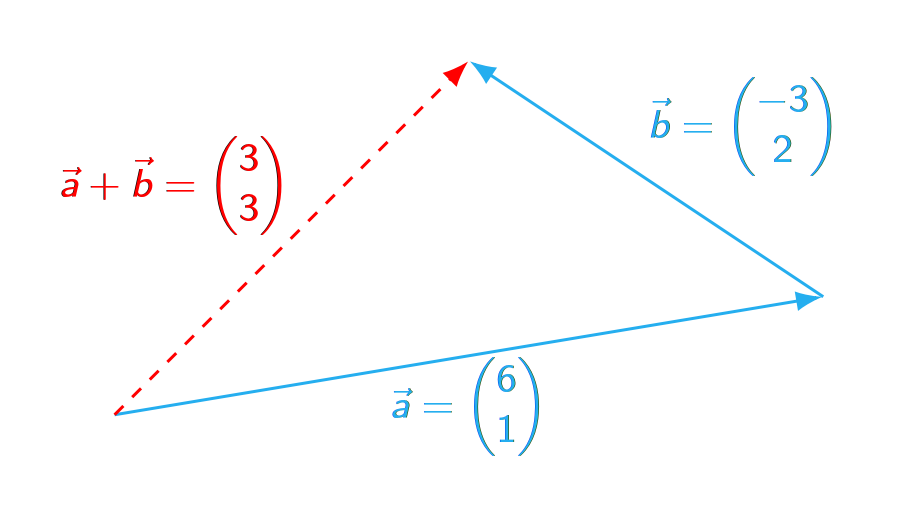
Beispiel
Du kannst an den violetten Punkten die Vektoren anpassen:
Dabei stellst du fest, dass die beiden roten Vektoren identisch sind.
Zum Herunterladen: addition.ggb
Sonderfall Nullvektor
Die Addition mit dem Nullvektor $\vec{0}=\begin{pmatrix}0\\0\\0\end{pmatrix}$ bewirkt nichts: $$\vec{a}+\vec{0}=\begin{pmatrix}a_1\\a_2\\a_3\end{pmatrix}+\begin{pmatrix}0\\0\\0\end{pmatrix}=\begin{pmatrix}a_1+0\\a_2+0\\a_3+0\end{pmatrix}=\begin{pmatrix}a_1\\a_2\\a_3\end{pmatrix}.$$
Gegenvektor
Zum Vektor $\vec{a} = \begin{pmatrix}a_1\\a_2\\a_3\end{pmatrix}$ gehört der Gegenvektor $-\vec{a} = \begin{pmatrix}-a_1\\-a_2\\-a_3\end{pmatrix}$. Die Vektorpfeile von $\vec{a}$ und $-\vec{a}$ sind gleich lang und verlaufen in genau entgegengesetzte Richtungen. Addiert man die beiden Vektoren, erhält man den Nullvektor.
Subtraktion zweier Vektoren
Wenn man sagt, dass man zwei Vektoren $\vec{a}=\begin{pmatrix}a_1\\a_2\\a_3\end{pmatrix}$ und $\vec{b}=\begin{pmatrix}b_1\\b_2\\b_3\end{pmatrix}$ subtrahiert, meint man damit, dass man deren einzelne Komponenten subtrahiert: $$\vec{a}-\vec{b}=\begin{pmatrix}a_1\\a_2\\a_3\end{pmatrix}-\begin{pmatrix}b_1\\b_2\\b_3\end{pmatrix}=\begin{pmatrix}a_1-b_1\\a_2-b_2\\a_3-b_3\end{pmatrix}.$$
Graphisch bedeutet die Subtraktion zweier Vektoren $\vec{a}=\begin{pmatrix}a_1\\a_2\\a_3\end{pmatrix}$ und $\vec{b}=\begin{pmatrix}b_1\\b_2\\b_3\end{pmatrix}$, dass der Verbindungsvektor von $\vec{b}$ nach $\vec{a}$ gebildet wird:
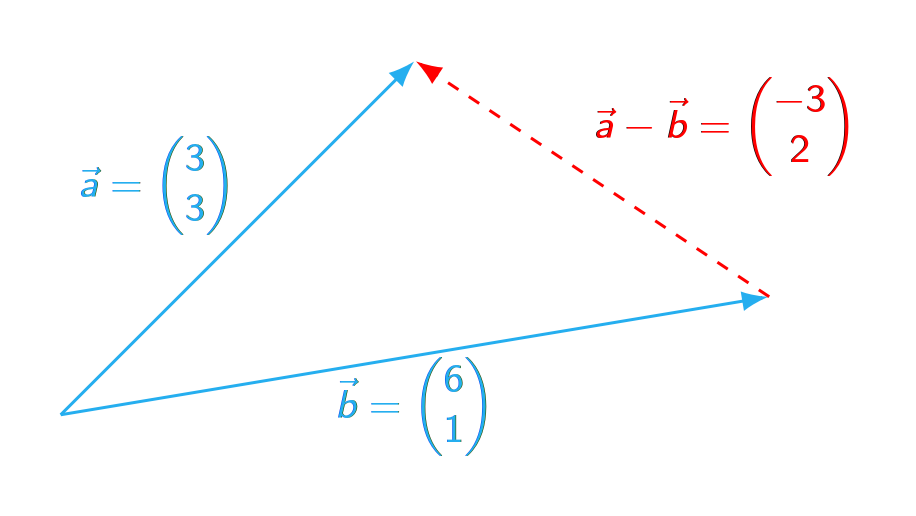
Beispiel
Du kannst an den violetten Punkten die Vektoren anpassen:
Zum Herunterladen: subtraktion.ggb

