Strukturierung – Überprüfung auf Parallelität
Vektoren bei der Überprüfung auf Parallelität verwenden
Die Parallelität von zwei Stecken lässt sich mit Hilfe der entsprechenden Vektoren überprüfen.
Aufgabe 1 (Einstieg)
Die Abbildung unter der Aufgabe zeigt etliche Streckenpaare (z.B. $\overline{AB}$ und $\overline{A'B'}$) mit den entsprechenden Vektoren. Stelle zunächst eine Vermutung auf, welche Strecken bzw. Vektoren parallel zueinander sind.
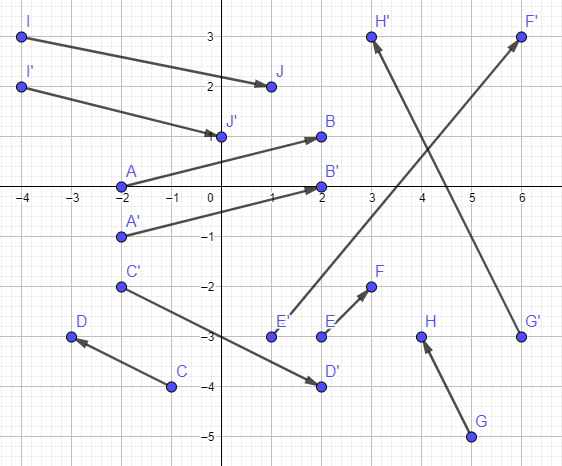
Aufgabe 2 (Erarbeitung)
(a) Bestimme die Koordinaten aller Vektoren. Was fällt auf? Erläutere, wie man anhand der Koordinaten der Vektoren erkennen kann, ob zwei Vektorpfeile (bzw. die zugehörigen Seiten) parallel sind.
(b) Gegeben ist eine Strecke $\overline{AB}$ durch die Punkte $A(-2|-1)$ und $B(4|1)$. Gesucht sind Strecken $\overline{CD}$, die parallel zur Strecke $\overline{AB}$ verlaufen. Bestimme zuerst mindestens 3 Strecken rechnerisch. Überprüfe dann mit einer exakten Zeichnung.
Den 3D-Fall betrachten
Kann man die Parallelität von Strecken im 3D-Fall analog zum 2D-Fall untersuchen? Um das herauszufinden, betrachte den folgenden Oktaeder. Man erhält ihn, wenn man die Seitenmitten benachbarter Seiten in einem Würfel verbindet.
Zum Herunterladen: oktaeder.ggb
Aufgabe 3 (Vertiefung)
(a) Die Kanten $\overline{LM}$ und $\overline{NJ}$ des Oktaeders scheinen parallel zu sein. Überprüfe das mit Hilfe der zugehörigen Vektoren.
(b) Im Würfel sind zusätzlich zwei Diagonalen $\overline{HB}$ und $\overline{GA}$ (gestrichelt) eingezeichnet. Ist die Oktaederkanten $\overline{LM}$ parallel zur Diagonalen $\overline{HB}$? Ist die Oktaederkanten $\overline{NL}$ parallel zur Diagonalen $\overline{GA}$? Begründe.
Einen Fachbegriff nutzen
Du hast du gesehen, dass man Parallelität von Strecken rechnerisch mit Hilfe zugehöriger Vektoren bestimmen kann. Man muss nur überprüfen, ob einer der Vektoren ein skalares Vielfaches des anderen ist. Die Eigenschaft „ist ein skalares Vielfaches“ von Vektoren werden wir noch häufiger benötigen. In der Mathematik ist es üblich, häufig benötigte Zusammenhänge mit einem Fachbegriff auszuzeichnen. Dafür müssen wir die Eigenschaft so genau wie möglich beschreiben:
Definition:
Zwei Vektoren $\vec{u}$ und $\vec{v}$ nennt man linear abhängig genau dann, wenn es eine reelle Zahl $k$ gibt, sodass $\vec{u} = k\cdot \vec{v}$ oder $\vec{v} = k\cdot \vec{u}$. Wir schreiben dann $\vec{u} \parallel \vec{v}$.
Zwei Vektoren $\vec{u}$ und $\vec{v}$ nennt man linear unabhängig genau dann, wenn sie nicht linear abhängig sind.
Aufgabe 4 (Sicherung)
(a) Formuliere eine Bedingung dafür, wie man überprüfen kann, ob $\overline{AB} \parallel \overline{CD}$. Benutze die soeben gelernten Fachbegriffe.
(b) Beim Thema Skalare Multiplikation wurde ein Wissensspeicher ausgefüllt. Dabei blieb die Box zur Parallelität leer. Fülle diese noch aus.
Lineare Abhängigkeit bzw. Parallelität systematisch überprüfen
Betrachte die beiden Vektoren $\vec{u} = \left(\begin{array}{c} 2 \\ -1 \\ 3 \end{array}\right)$ und $\vec{v} = \left(\begin{array}{c} -3 \\ 1.5 \\ -4 \end{array}\right)$. Sind die Vektoren linear abhängig bzw. sind die zugehörigen Vektorpfeile parallel?
Eine mögliche Argumentation sieht so aus: „Damit die Vektorpfeile parallel sind, müssten folgende Bedingungen mit einer reellen Zahl $k$ erfüllt sein:“
$\vec{v} = k \cdot \vec{u}$ bzw.
$\left(\begin{array}{c} -3 \\ 1.5 \\ -4 \end{array}\right) = k \cdot \left(\begin{array}{c} 2 \\ -1 \\ 3 \end{array}\right)$ bzw.
$\left(\begin{array}{c} -3 \\ 1.5 \\ -4 \end{array}\right) = \left(\begin{array}{c} k \cdot 2 \\ k \cdot (-1) \\ k \cdot 3 \end{array}\right)$ bzw.
$\begin{array}{lrcrcrcr} [1] &\quad -3 & = & 2k \\ [2] &\quad 1.5 & = & -k \\ [3] &\quad -4 & = & 3k \end{array}$
Aufgabe 5 (Vertiefung)
(a) Erläutere zunächst die Argumentation im Beispiel.
(b) Gibt es die Zahl $k$ hier? Argumentiere mit den Gleichungen des Gleichungssystems.
