Einstieg - Ein Zahlenadditionsverfahren
Mit einem Zahlenadditionsverfahren verschlüsseln
Im Laufe der Zeit wurden sehr viele Verschlüsselungsverfahren entwickelt. Wir betrachten hier zunächst ein sehr einfaches Verschiebeverfahren, das an das Caesar-Verfahren angelehnt ist.
Die Grundidee besteht darin, die Zeichen des Quelltextes in Zahlen umzuwandeln und diese Zahlen anschließend um eine gewählte Schlüsselzahl zu erhöhen.
Verschlüsselung mit dem Zahlenadditionsverfahren
Schritt 1: Codierung
Alle Zeichen des Quelltextes werden in Zahlen umgewandelt.
Zur Umwandlung wird die ASCII-Tabelle benutzt.
Schritt 2: Verschlüsselung
Zu allen Zahlen im Quellcode $C$ wird die gewählte Schlüsselzahl $s$ hinzuaddiert. Kurz: $C' = C + s$.
Aufgabe 1
Teste das Zahlenadditionsverfahren mit dem folgenden Applet.
Zum Herunterladen: verschluesselung1a.ggb
Mit dem Zahlenadditionsverfahren entschlüsseln
Die Entschlüsselung beim Zahlenadditionsverfahren funktioniert ganz analog zum Verschlüsseln. Zu den Zahlen im Geheimcode wird eine Gegenschlüsselzahl hinzuaddiert.
Entschlüsselung mit dem Zahlenadditionsverfahren
Schritt 1: Entschlüsselung
Zu allen Zahlen im Geheimcode $C'$ wird die Gegenschlüsselzahl $s'$ hinzuaddiert. Kurz: $C = C' + s'$.
Schritt 2: Decodierung
Alle Zahlen aus dem Geheimcode werden in Zeichen umgewandelt.
Zur Umwandlung wird die ASCII-Tabelle benutzt.
Aufgabe 2
(a) Teste das Entschlüsseln mit dem folgenden Applet. Folgende Info ist bekannt: Bei der Verschlüsselung wurde die Schlüsselzahl $s = 27$ benutzt. Gib den passenden Gegenschlüssel im entsprechenden Eingabefeld ein. Wenn dieser richtig gewählt ist, dann kann man den Quelltext verstehen.
Zum Herunterladen: entschluesselung1a.ggb
(b) Erläutere anhand des Beispiels: Das Zahlenadditionsverfahren ist alles andere als sicher. Wenn man den Schlüssel kennt, mit dem ein Quelltext verschlüsselt wurde, dann kann man direkt den Gegenschlüssel erzeugen und damit den Quelltext aus dem Geheimcode rekonstruieren.
Das Gegenzahlprinzip beim Zahlenadditionsverfahren verwenden
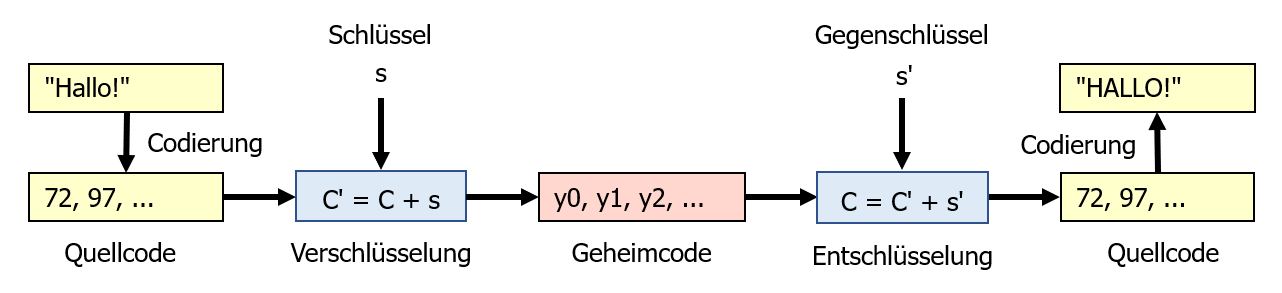
Die Übersicht verdeutlicht noch einmal das Ver- und Entschlüsseln beim Zahlenadditionsverfahren.
Der Gegenschlüssel $s'$ beim Entschlüsseln muss so gewählt werden, dass er die Verschiebung mit dem Schlüssel $s$ rückgängig macht. Es muss also $s + s' = 0$ bzw. $s' = -s$ gelten. Der Gegenschlüssel muss demnach die Gegenzahl zum Schlüssel sein.
Aufgabe 3
Wenn man erst verschlüsselt und anschließend entschlüsselt, dann sollte der Ausgangscode wieder entstehen. Erläutere das anhand der folgenden Übersicht mit Hilfe des Gegenzahlprinzips.
$\begin{array}{ll} C &\\ \downarrow & \text{Verschlüsselung mit } s \\ C + s &\\ \downarrow & \text{Entschlüsselung mit } s' \\ (C + s) + s' &\\ \downarrow & \text{Umformung mit dem Assoziativgesetz} \\ C + (s + s') &\\ \downarrow & \text{Gegenschlüsselprinzip: } s + s' = 0 bzw. s' = -s \\ C + 0 \\ \downarrow & \text{Nullverschiebung} \\ C \end{array}$
Quellen
- [1]: Verschlüsselung mit dem Zahlenadditionsverfahren - Urheber: KB -