Vertiefung
Zur Orientierung
Im letzten Abschnitt hast du algebraische Beschreibung für spezielle Drehungen und Spiegelungen entwickelt. Hier betrachten wir jetzt beliebige Drehungen um den Koordinatenursprung und Spiegelungen an beliebigen Ursprungsgeraden.
Drehungen algebraisch beschreiben
Wir betrachten eine Drehung mit einem beliebigen Drehwinkel $\alpha$ und dem Ursprung als Drehzentrum.
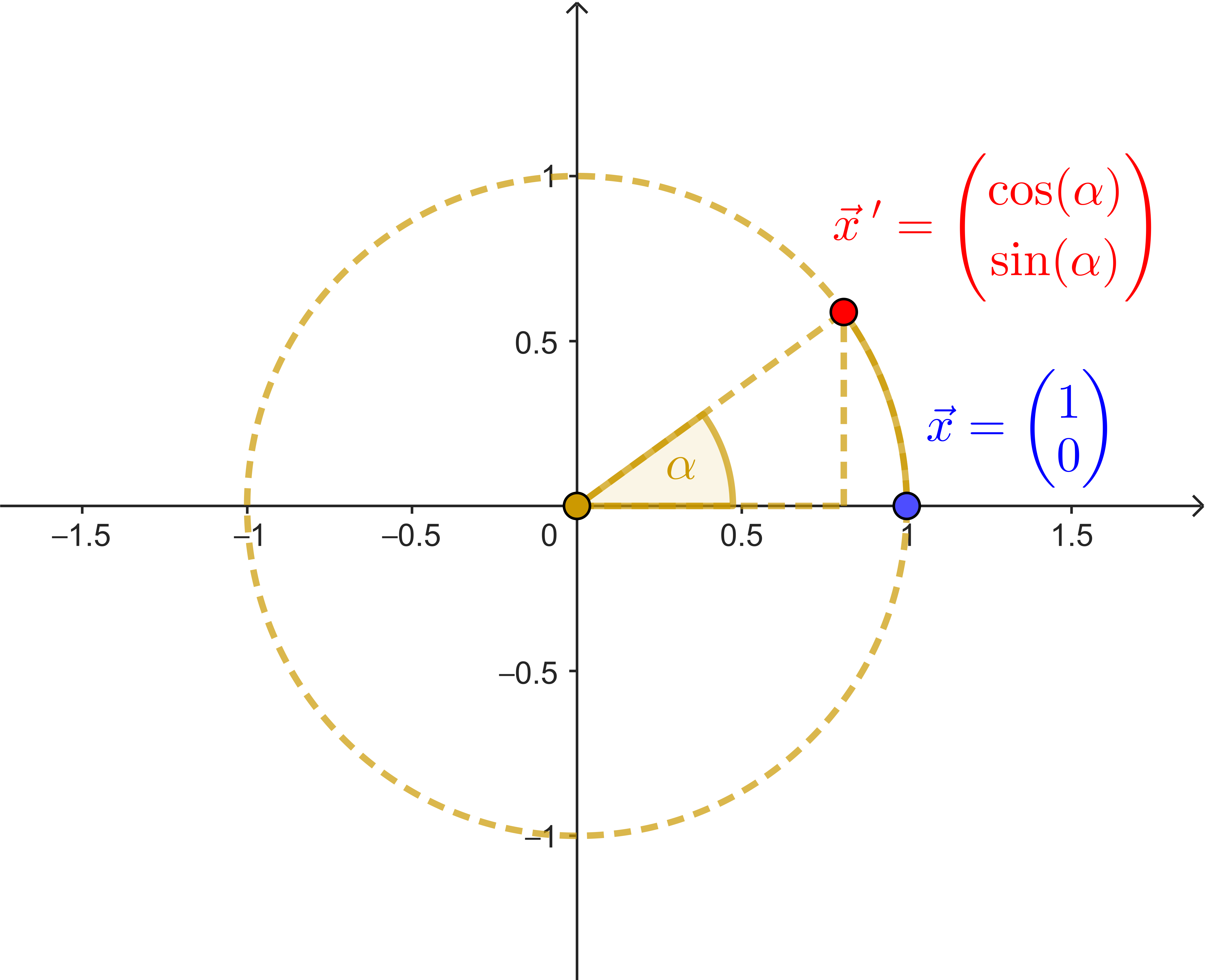
|
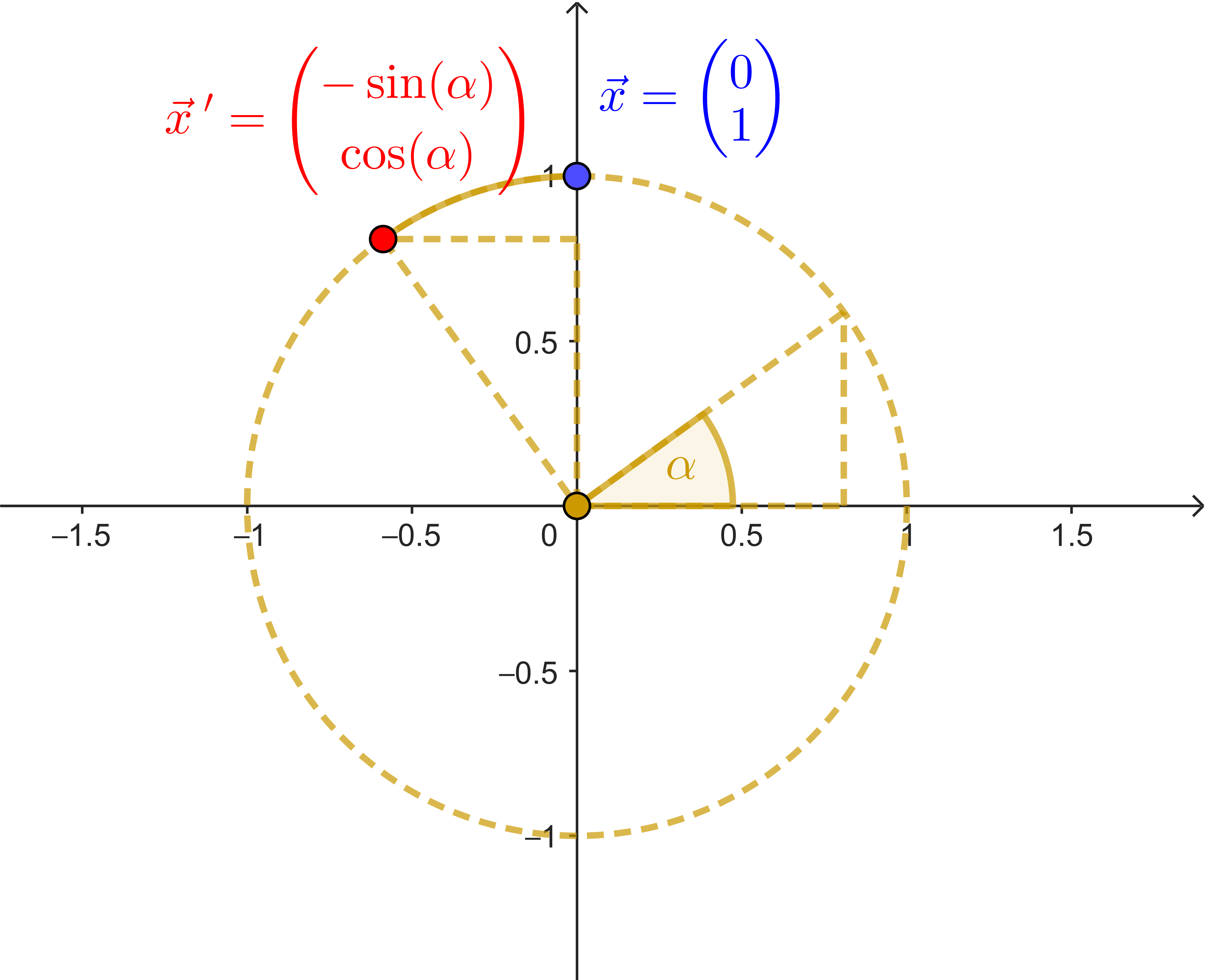
|
| $\begin{pmatrix} 1 \\ 0 \end{pmatrix} \rightarrow \begin{pmatrix} \cos(\alpha) \\ \sin(\alpha) \end{pmatrix}$ | $\begin{pmatrix} 0 \\ 1 \end{pmatrix} \rightarrow \begin{pmatrix} -\sin(\alpha) \\ \cos(\alpha) \end{pmatrix}$ |
Aufgabe 1 (★★★)
(a) Betrachte den Punkt $X$ mit $\vec{x} = \begin{pmatrix} 1 \\ 0 \end{pmatrix}$. Begründe mit der Abbildung oben, dass man für den Bildpunkt $X'$ dann $\vec{x}' = \begin{pmatrix} \cos(\alpha) \\ \sin(\alpha) \end{pmatrix}$ erhält.
(b) Betrachte den Punkt $X$ mit $\vec{x} = \begin{pmatrix} 0 \\ 1 \end{pmatrix}$. Begründe mit der Abbildung oben, dass man für den Bildpunkt $X'$ dann $\vec{x}' = \begin{pmatrix} -\sin(\alpha) \\ \cos(\alpha) \end{pmatrix}$ erhält.
(c) Begründe: Die folgenden Formeln liefern die Ergebnisse aus (a) und (b).
Drehung (gegen den Uhrzeigersinn) um den Ursprung mit dem Drehwinkel $\alpha$
$x_1' = \cos(\alpha) \cdot x_1 -\sin(\alpha)\cdot x_2$
$x_2' = \sin(\alpha) \cdot x_1 + \cos(\alpha)\cdot x_2$
(d) Teste die Formeln im Applet unten. Im Applet ist im oberen Fenster bereits ein Drehwinkel eingestellt. Im unteren Fenster sind die Ausgangsfigur (blau dargestellt) und die gedrehte Figur (rot dargestellt) zu sehen. Zusätzlich ist eine violett dargestellte Figur zu sehen, die ebenfalls gedreht werden soll – aber mit algebraischen Mitteln. Trage in den Eingabefeldern die Formeln (passend zum eingestellten Drehwinkel) ein. Aktiviere die Kontrollfigur. Bei korrekter Eingabe deckt sich die Kontrollfigur mit der verschobenen Figur.
Spiegelungen algebraisch beschreiben
Wir betrachten eine Spiegelung an einer Ursprungsgeraden, die mit der $x$-Achse einen Winkel $\alpha$ einschließt.
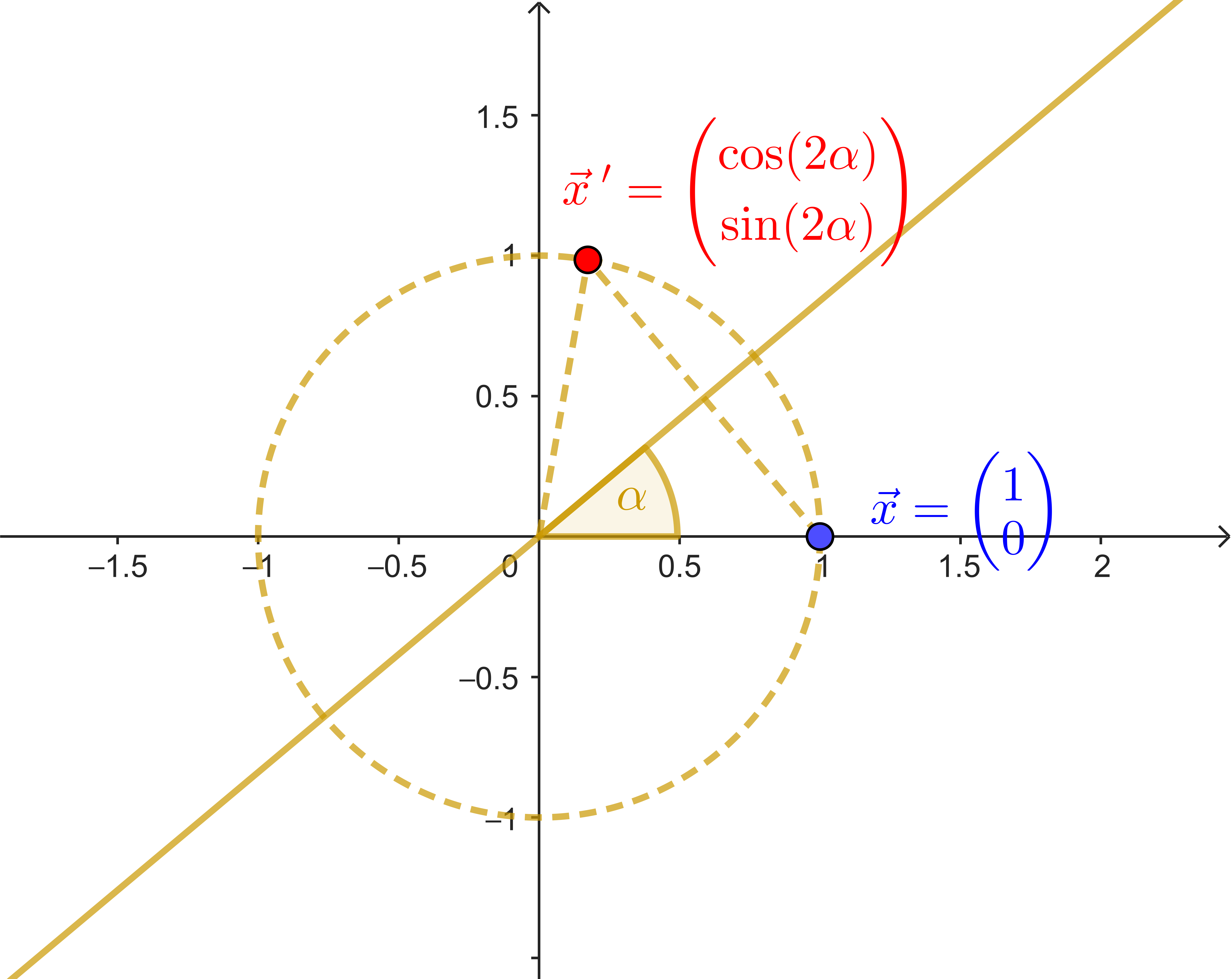
|
|
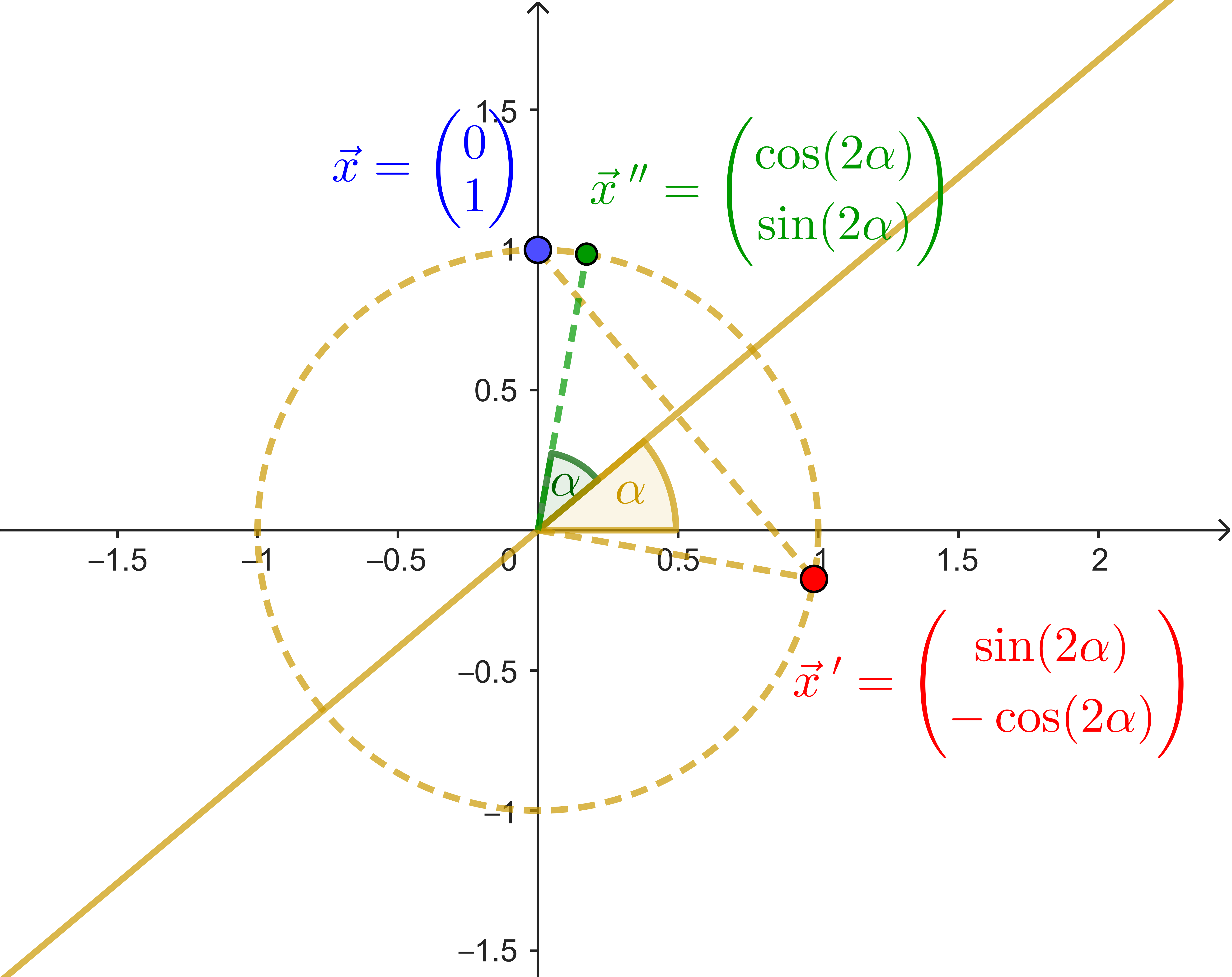
| $\begin{pmatrix} 1 \\ 0 \end{pmatrix} \rightarrow \begin{pmatrix} \cos(2\alpha) \\ \sin(2\alpha) \end{pmatrix}$ | $\begin{pmatrix} 0 \\ 1 \end{pmatrix} \rightarrow \begin{pmatrix} \sin(2\alpha) \\ -\cos(2\alpha) \end{pmatrix}$ |
Aufgabe 2 (★★★)
(a) Betrachte den Punkt $X$ mit $\vec{x} = \begin{pmatrix} 1 \\ 0 \end{pmatrix}$. Begründe mit der Abbildung oben, dass man für den Bildpunkt $X'$ dann $\vec{x}' = \begin{pmatrix} \cos(2\alpha) \\ \sin(2\alpha) \end{pmatrix}$ erhält.
(b) Betrachte den Punkt $X$ mit $\vec{x} = \begin{pmatrix} 0 \\ 1 \end{pmatrix}$. Begründe mit der Abbildung oben, dass man für den Bildpunkt $X'$ dann $\vec{x}' = \begin{pmatrix} \sin(2\alpha) \\ -\cos(2\alpha) \end{pmatrix}$ erhält.
(c) Begründe: Die folgenden Formeln liefern die Ergebnisse aus (a) und (b).
Spiegelung an einer Ursprungsgeraden, die den Winkel $\alpha$ mit der $x$-Achse einschließt
$x_1' = \cos(2\alpha) \cdot x_1 + \sin(2\alpha)\cdot x_2$
$x_2' = \sin(2\alpha) \cdot x_1 - \cos(2\alpha)\cdot x_2$
(d) Teste die Formeln im Applet unten. Im Applet ist im oberen Fenster bereits eine Ursprungsgerade eingestellt. Im unteren Fenster sind die Ausgangsfigur (blau dargestellt) und die gespiegelte Figur (rot dargestellt) zu sehen. Zusätzlich ist eine violett dargestellte Figur zu sehen, die ebenfalls gespiegelt werden soll – aber mit algebraischen Mitteln. Trage in den Eingabefeldern die Formeln (passend zur eingestellten Ursprungsgerade) ein. Aktiviere die Kontrollfigur. Bei korrekter Eingabe deckt sich die Kontrollfigur mit der verschobenen Figur.

