Erarbeitung
Zur Orientierung
Hier geht es darum, das Umkehren von geometrischen Abbildungen algebraisch durchzuführen.
Eine Abbildung umkehren
Wir betrachten die folgende Abbildung:
$\alpha: \begin{pmatrix} x_1' \\ x_2' \end{pmatrix} = \begin{pmatrix} 1 & -2 \\ 2 & 1 \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}$
Die Umkehrabbildung $\alpha^{-1}$ beschreibt die umgekehrte Zuordnung von Vektoren bzgl. $\alpha$ . In der Übersicht sind einige exemplarische Zuordnungen aufgeführt.
| Abbildung | Umkehrabbildung |
|---|---|
|
|
|
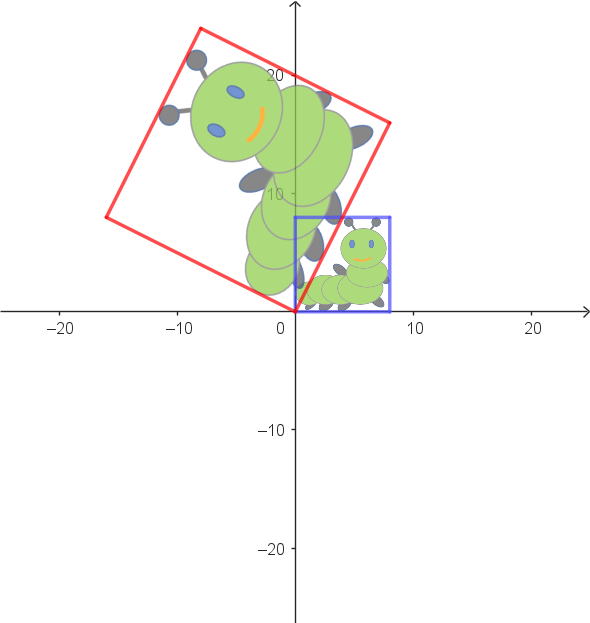
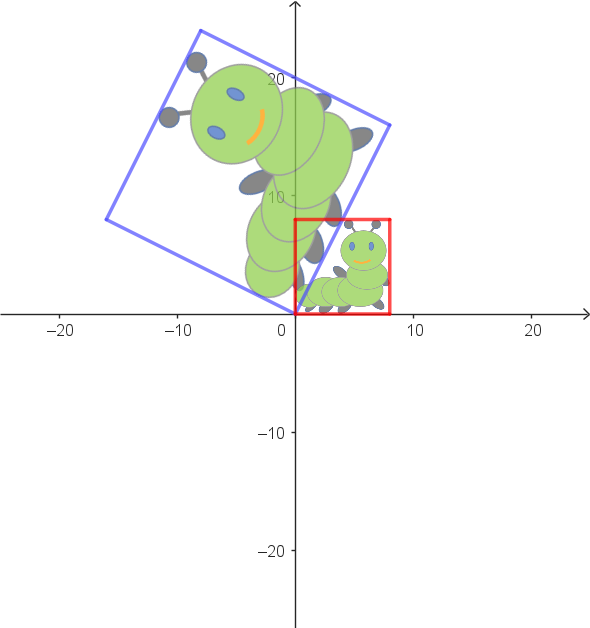
$\alpha: \begin{pmatrix} 8 \\ 0 \end{pmatrix} \rightarrow \begin{pmatrix} 8 \\ 16 \end{pmatrix}$ $\alpha: \begin{pmatrix} 0 \\ 8 \end{pmatrix} \rightarrow \begin{pmatrix} -16 \\ 8 \end{pmatrix}$ |
$\alpha^{-1}: \begin{pmatrix} 8 \\ 16 \end{pmatrix} \rightarrow \begin{pmatrix} 8 \\ 0 \end{pmatrix}$ $\alpha^{-1}: \begin{pmatrix} -16 \\ 8 \end{pmatrix} \rightarrow \begin{pmatrix} 0 \\ 8 \end{pmatrix}$ |
Aufgabe 1
Verdeutliche die in der Übersicht aufgeführten Zuordnungen anhand der Grafiken. Ergänze weitere Zuordnungen mit ihren Umkehrungen in der Übersicht.
Eine Umkehrabbildung bestimmen
Ziel ist es, eine Vektorgleichung zur Beschreibung der Umkehrabbildung $\alpha^{-1}$ zu bestimmen. Der folgende Ansatz geht davon aus, dass $\alpha^{-1}$ ebenfalls eine lineare Abbildung ist. Ob das gerechtfertigt ist, muss sich noch zeigen.
$\alpha^{-1}: \begin{pmatrix} x_1' \\ x_2' \end{pmatrix} = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}$
Die Umkehrabbildung $\alpha^{-1}$ soll die in der Übersicht bereits aufgestellten Bedingungen erfüllen:
$\alpha^{-1}: \begin{pmatrix} 8 \\ 16 \end{pmatrix} \rightarrow \begin{pmatrix} 8 \\ 0 \end{pmatrix}$ bzw. $\alpha^{-1}: \begin{pmatrix} -16 \\ 8 \end{pmatrix} \rightarrow \begin{pmatrix} 0 \\ 8 \end{pmatrix}$
Aufgabe 1
Die Bedingungen kann man in ein lineares Gleichungssystem überführen. Ergänze hierzu die Einträge in der folgenden Übersicht.
| Bedingung | Vektorgleichung | Koordinatengleichungen |
|---|---|---|
| $\alpha^{-1}: \begin{pmatrix} 8 \\ 16 \end{pmatrix} \rightarrow \begin{pmatrix} 8 \\ 0 \end{pmatrix}$ | $\begin{pmatrix} a & b \\ c & d \end{pmatrix} \cdot \begin{pmatrix} 8 \\ 16 \end{pmatrix} = \begin{pmatrix} 8 \\ 0 \end{pmatrix}$ | $\begin{array}{lrcrcrcr} [1] &\quad 8a & + & 16b & = & 8 \\ [2] &\quad \dots & + & \dots & = & \dots \end{array}$ |
| $\alpha^{-1}: \begin{pmatrix} -16 \\ 8 \end{pmatrix} \rightarrow \begin{pmatrix} 0 \\ 8 \end{pmatrix}$ | $\dots$ | $\begin{array}{lrcrcrcr} [3] &\quad \dots & + & \dots & = & \dots \\ [4] &\quad \dots & + & \dots & = & \dots \end{array}$ |
Aufgabe 2
Löse das entstehende lineare Gleichungssystem.
Aufgabe 3
Setze die ermittelten Werte für $a$, $b$, $c$, $d$ in die Abbildungsgleichung ein.
$\alpha^{-1}: \begin{pmatrix} x_1' \\ x_2' \end{pmatrix} = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}$
Wenn die Werte für $a$, $b$, $c$, $d$ korekt bestimmt sind, dann gilt $\alpha^{-1}: \begin{pmatrix} 8 \\ 16 \end{pmatrix} \rightarrow \begin{pmatrix} 8 \\ 0 \end{pmatrix}$ sowie $\alpha^{-1}: \begin{pmatrix} -16 \\ 8 \end{pmatrix} \rightarrow \begin{pmatrix} 0 \\ 8 \end{pmatrix}$. Aber, liefert $\alpha^{-1}$ auch für andere Zuordnungen die richtigen Umkehrungen? Überprüfe das mit dem Applet.
Führe zunächst die Ausgangsabbildung $\alpha$ (mit passenden Einstellungen für $a$, $b$, $c$, $d$) aus. Drücke [neue Ausgangsposition]. Führe anschließend die Abbildung $\alpha^{-1}$ (mit passenden Einstellungen für $a$, $b$, $c$, $d$) aus.
Zum Herunterladen: affineabbildungen_dynamisch_1.ggb
Einen problematischen Fall betrachten
Im Beispiel oben ist es gelungen, die Umkehrabbildung zu einer vorgegebenen linearen Abbildung zu bestimmen. Aber, klappt das immer? Führe im Applet die folgende Abbildung aus. Was ist hier anders als im Beispiel oben?
$\alpha: \begin{pmatrix} x_1' \\ x_2' \end{pmatrix} = \begin{pmatrix} 1 & 2 \\ 0.5 & 1 \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}$
Aufgabe 4
Begründe, dass man diese Abbildung nicht umkehren kann. Betrachte z.B. die folgenden Zuordnungen.
$\alpha^{-1}: \begin{pmatrix} 8 \\ 0 \end{pmatrix} \rightarrow \begin{pmatrix} \dots \\ \dots \end{pmatrix}$
$\alpha^{-1}: \begin{pmatrix} 0 \\ 4 \end{pmatrix} \rightarrow \begin{pmatrix} \dots \\ \dots \end{pmatrix}$

