o-mathe | Geometrische Deutung von Vektoren » Übungen

Übungen - Geometrische Deutung von Vektoren

Aufgabe 1

Eine Drohne soll die Route Haus des Nikolaus abfliegen.

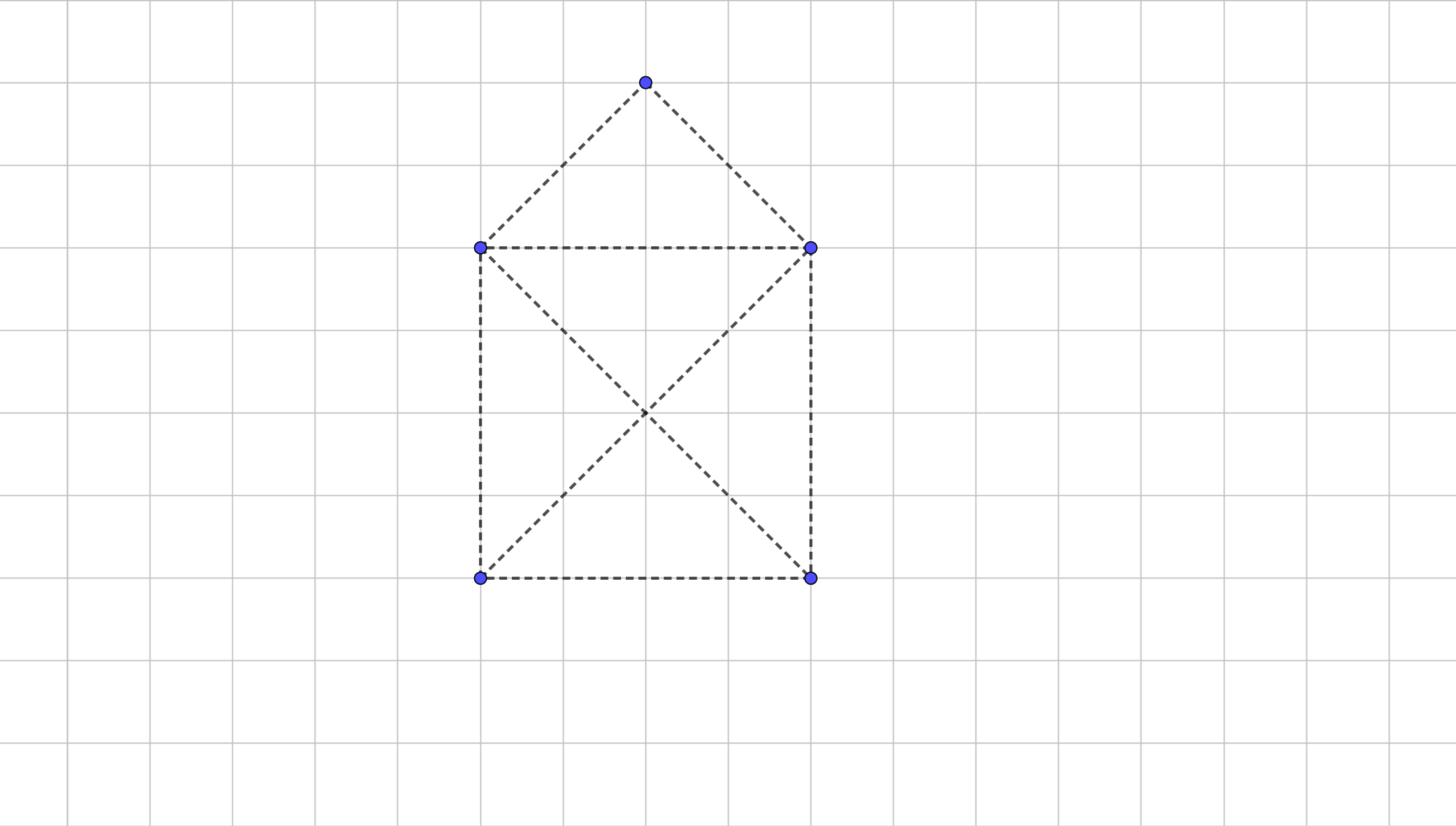
Erstelle einen Flugplan für dieser Route. Den Startpunkt $(a_{1}, a_{2})$ und die Länge der Teilabstände kannst du frei wählen.

$(\begin{matrix} a_{1} \\ a_{2} \end{matrix}) \overset{(\begin{matrix} \dots \\ \dots \end{matrix})}{⟶} (\begin{matrix} \dots \\ \dots \end{matrix}) \overset{(\begin{matrix} \dots \\ \dots \end{matrix})}{⟶} \dots$

Teste deinen Flugbahn im Applet.

Applet einblenden

Zum Herunterladen: drohne2dv1.ggb

Aufgabe 2

In der Grafik wird eine Verschiebung mit Hilfe einer Ausgangs- und verschobenen Figur beschrieben.

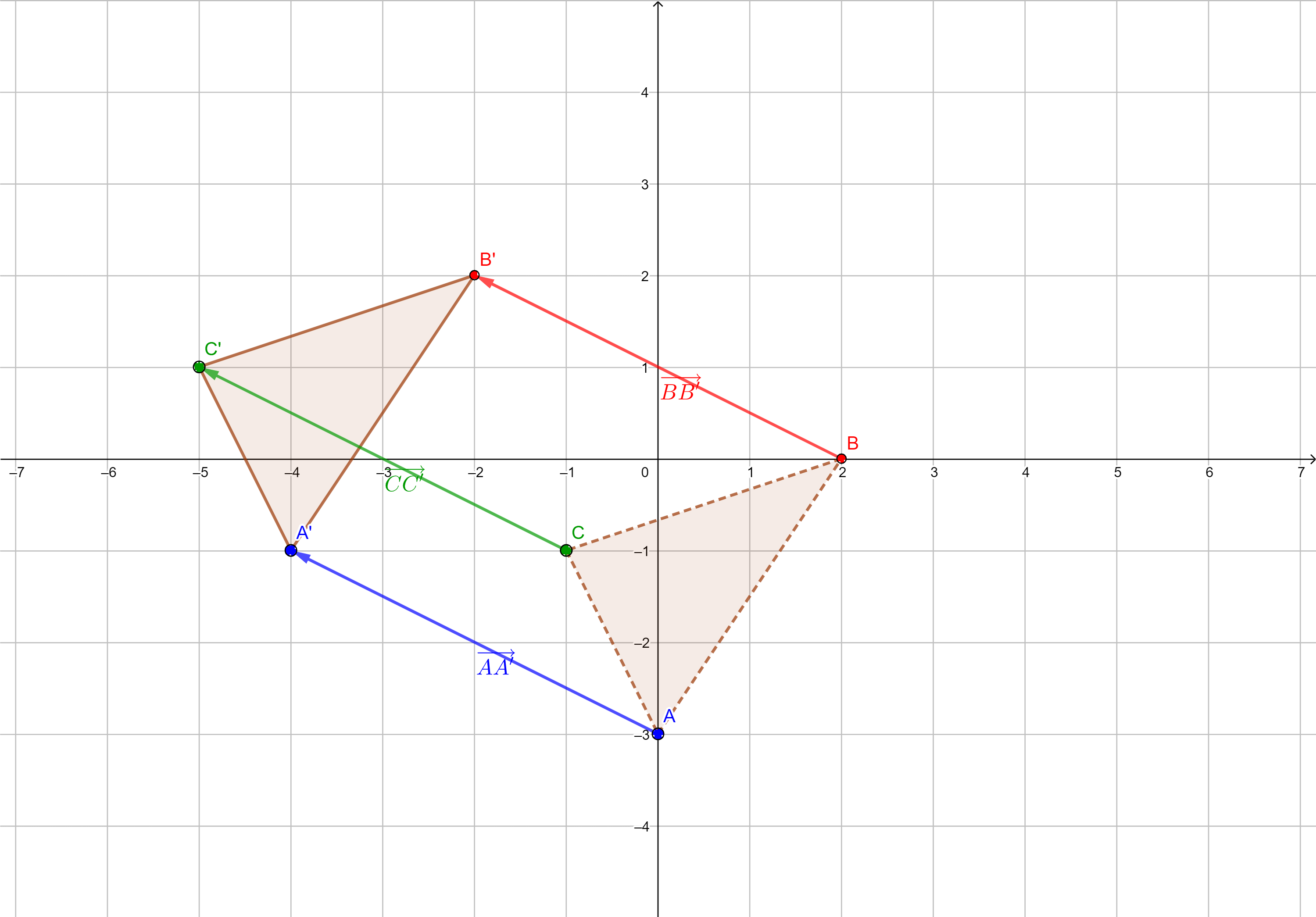
(a) Beschreibe die Verschiebung exemplarisch mit Hilfe von Zuordnungen von Punkten.

$\underset{\vec{a}}{\underset{⏟}{(\begin{matrix} \dots \\ \dots \end{matrix})}} \overset{(\begin{matrix} \dots \\ \dots \end{matrix})}{⟶} \underset{\vec{a}^{'}}{\underset{⏟}{(\begin{matrix} \dots \\ \dots \end{matrix})}}$
$\underset{\vec{b}}{\underset{⏟}{(\begin{matrix} \dots \\ \dots \end{matrix})}} \overset{(\begin{matrix} \dots \\ \dots \end{matrix})}{⟶} \underset{\vec{b}^{'}}{\underset{⏟}{(\begin{matrix} \dots \\ \dots \end{matrix})}}$
$\underset{\vec{c}}{\underset{⏟}{(\begin{matrix} \dots \\ \dots \end{matrix})}} \overset{(\begin{matrix} \dots \\ \dots \end{matrix})}{⟶} \underset{\vec{c}^{'}}{\underset{⏟}{(\begin{matrix} \dots \\ \dots \end{matrix})}}$

(b) Erläutere anhand der betrachteten Verschiebung:

Die Verschiebung kann man mit einem Vektor beschreiben.
Die Verschiebung einzelner Punkte kann man rechnerisch mit Vektoren durchführen.

Aufgabe 3

In der Tabelle werden Punkte und Verschiebungen mit Hilfe von Vektoren beschrieben. Ergänze jeweils die fehlenden Koordinaten.

Aufgabe	Verschiebung	Koordinaten der Vektoren
(a)	$(\begin{matrix} 2 \\ - 2 \end{matrix}) \overset{(\begin{matrix} 1 \\ 3 \end{matrix})}{⟶} (\begin{matrix} e_{1} \\ e_{2} \end{matrix})$	$e_{1} =$ $e_{2} =$
(b)	$(\begin{matrix} 4 \\ 4 \end{matrix}) \overset{(\begin{matrix} v_{1} \\ v_{2} \end{matrix})}{⟶} (\begin{matrix} 5 \\ 2 \end{matrix})$	$v_{1} =$ $v_{2} =$
(c)	$(\begin{matrix} a_{1} \\ a_{2} \end{matrix}) \overset{(\begin{matrix} 3 \\ - 1 \end{matrix})}{⟶} (\begin{matrix} - 2 \\ 4 \end{matrix})$	$a_{1} =$ $a_{2} =$
(d)	$(\begin{matrix} 1 \\ 3 \end{matrix}) \overset{(\begin{matrix} 4 \\ - 2 \end{matrix})}{⟶} \overset{(\begin{matrix} - 2 \\ 1 \end{matrix})}{⟶} (\begin{matrix} e_{1} \\ e_{2} \end{matrix})$	$e_{1} =$ $e_{2} =$
(e)	$(\begin{matrix} a_{1} \\ a_{2} \end{matrix}) \overset{(\begin{matrix} - 4 \\ 3 \end{matrix})}{⟶} \overset{(\begin{matrix} v_{1} \\ v_{2} \end{matrix})}{⟶} (\begin{matrix} a_{1} \\ a_{2} \end{matrix})$	$v_{1} =$ $v_{2} =$
(f)	$(\begin{matrix} 6 \\ 5 \end{matrix}) \overset{- (\begin{matrix} 2 \\ - 3 \end{matrix})}{⟶} (\begin{matrix} e_{1} \\ e_{2} \end{matrix})$	$e_{1} =$ $e_{2} =$
(g)	$(\begin{matrix} 9 \\ 0 \end{matrix}) \overset{2 \cdot (\begin{matrix} v 1 \\ v_{2} \end{matrix})}{⟶} (\begin{matrix} 5 \\ 6 \end{matrix})$	$v_{1} =$ $v_{2} =$

Aufgabe 4

Was beschreibt die folgende Gleichung? Verdeutliche mit Hilfe konkreter Zahlenwerte und allgemein anhand einer Skizze.

$\vec{A B} + \vec{B C} + \vec{C A} = \vec{A A}$

Aufgabe 5

Die Punkte $A$ und $B$ legen eine Strecke fest. Der Punkt $M$ ist der Mittelpunkt dieser Strecke. Im Applet kannst du die Lage der Punkte $A$ und $B$ variieren.

Zum Herunterladen: mittelpunkt.ggb

Ziel ist es, Formeln zur Berechnung von $M$ aus den vorgegebenen Endpunkten $A$ und $B$ der Strecke zu entwickeln.

(a) Gib für $X$ und $Y$ die passenden Punkte an:

$\vec{m} = \vec{a} + \frac{1}{2} \cdot \vec{X Y}$

(b) Begründe:

$\vec{m} = \vec{a} + \frac{1}{2} \cdot (\vec{b} - \vec{a})$

(c) Leite mit den Rechengesetzen für Vektoren her:

$\vec{m} = \frac{1}{2} (\vec{a} + \vec{a})$

(d) Teste die Formeln mit konkreten Fallbeispielen im Applet. Dokumentiere jeweils ein typisches Testbeispiel.