o-mathe | Umkehrung affiner Abbildungen » Zusammenfassung

Zusammenfassung - Umkehrung affiner Abbildungen

Die Grundidee

Die Umkehrabbildung $α^{- 1}$ zu einer vorgegebenen (geometrischen) Abbildung $α$ kehrt die Zuordnungen der vorgegebenen Abbildung $α$ alle um – sofern dies möglich ist.

Beispiel 1: umkehrbare Abbildung

Abbildung	Umkehrabbildung

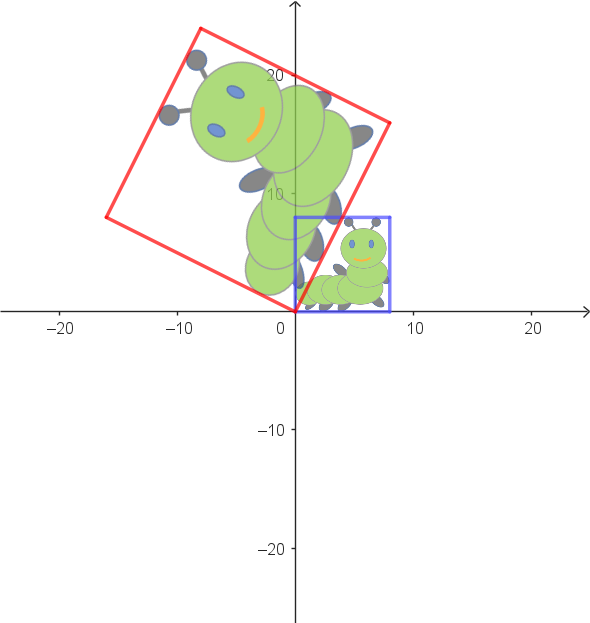
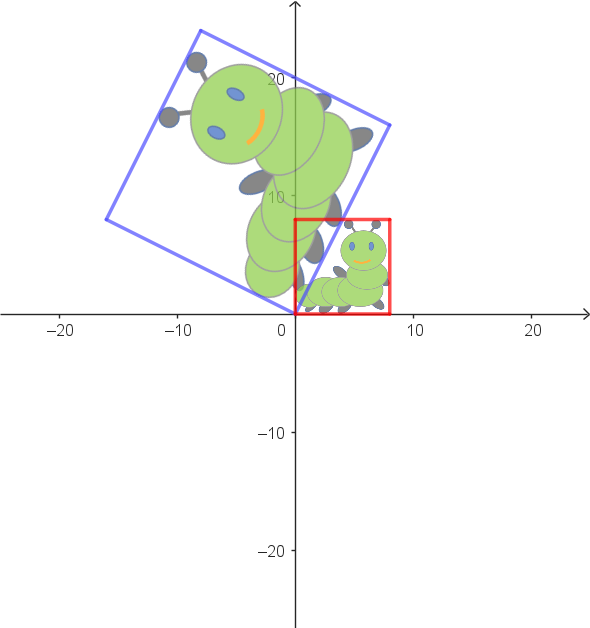
Zuordnungsbeispiele: $α : (\begin{matrix} 8 \\ 0 \end{matrix}) \to (\begin{matrix} 8 \\ 16 \end{matrix})$ $α : (\begin{matrix} 0 \\ 8 \end{matrix}) \to (\begin{matrix} - 16 \\ 8 \end{matrix})$	Zuordnungsbeispiele: $α^{- 1} : (\begin{matrix} 8 \\ 16 \end{matrix}) \to (\begin{matrix} 8 \\ 0 \end{matrix})$ $α^{- 1} : (\begin{matrix} - 16 \\ 8 \end{matrix}) \to (\begin{matrix} 0 \\ 8 \end{matrix})$
Vektorgleichung als allgemeine Zuordnungsvorschrift: $α : (\begin{matrix} x_{1}^{'} \\ x_{2}^{'} \end{matrix}) = (\begin{matrix} 1 & - 2 \\ 2 & 1 \end{matrix}) \cdot (\begin{matrix} x_{1} \\ x_{2} \end{matrix})$	Vektorgleichung als allgemeine Zuordnungsvorschrift: $α^{- 1} : (\begin{matrix} x_{1}^{'} \\ x_{2}^{'} \end{matrix}) = (\begin{matrix} 0.2 & 0.4 \\ - 0.4 & 0.2 \end{matrix}) \cdot (\begin{matrix} x_{1} \\ x_{2} \end{matrix})$

Die Abbildung $α$ in Beispiel 1 ist umkehrbar. Die Abbildung $α^{- 1}$ ist die Umkehraabildung zur Abbildung $α$ . Wie man sie bestimmen kann, wird weiter unten erläutert.

Beispiel 2: nicht umkehrbare Abbildung

Abbildung	Umkehrabbildung

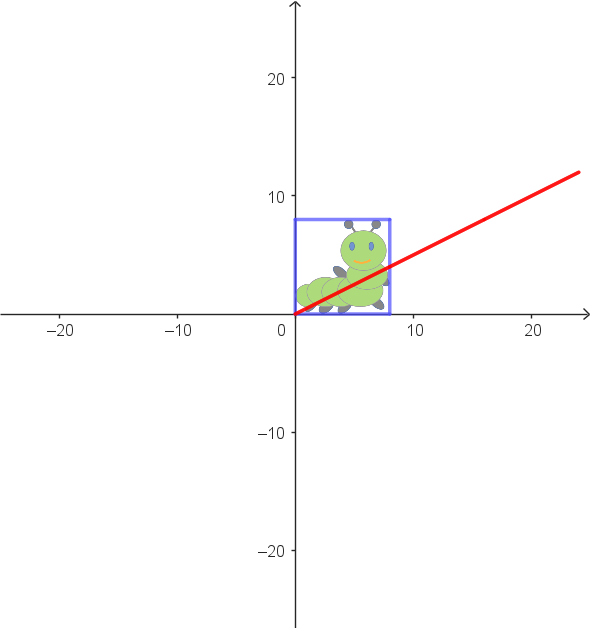
Zuordnungsbeispiele: $α : (\begin{matrix} 8 \\ 0 \end{matrix}) \to (\begin{matrix} 8 \\ 4 \end{matrix})$ $α : (\begin{matrix} 0 \\ 4 \end{matrix}) \to (\begin{matrix} 8 \\ 4 \end{matrix})$	Zuordnungsbeispiele: $α^{- 1} : (\begin{matrix} 8 \\ 4 \end{matrix}) \to ?$
Vektorgleichung als allgemeine Zuordnungsvorschrift: $α : (\begin{matrix} x_{1}^{'} \\ x_{2}^{'} \end{matrix}) = (\begin{matrix} 1 & 2 \\ 0.5 & 1 \end{matrix}) \cdot (\begin{matrix} x_{1} \\ x_{2} \end{matrix})$	Vektorgleichung als allgemeine Zuordnungsvorschrift: $α^{- 1}$ existiert nicht

Nicht jede (lineare) Abbildung ist umkehrbar. Die Abbildung $α$ in Beispiel 2 ist nicht umkehrbar. Das erkennt man anhand von Zuordnungen, die zum selben Bildvektor führen.

Beschreibung mit Fachbegriffen

Wir präzisieren die bereits (intuitiv) verwendeten Begriffe.

Umkehrabbildung

Eine geometrische Abbildung $α$ ist umkehrbar genau dann, wenn sie unterschiedliche Vektoren (bzw. Punkte) jeweils auf unterschiedliche Bildvektoren (bzw. Bildpunkte) abbildet.

Die Umkehrbarabbildung $α^{- 1}$ zu einer vorgegebenen geometrischen Abbildung $α$ kehrt die Zuordnungen der vorgegebenen Abbildung $α$ alle um – sofern die Abbildung umkehrbar ist.

Das Zusammenspiel von Abbildung und Umkehrabbildung lässt sich auch so beschreiben: Wenn man zuerst die Abbildung $α$ auf einen Vektor anwendet und anschließend die Umkehrabbildung $α^{- 1}$ auf den Bildvektor, dann erhält man wieder den Ausgangsvektor.

In Beispiel 1 sieht man das anhand ausgewählter Zuordnungen:

$(\begin{matrix} 8 \\ 0 \end{matrix}) \overset{α}{⟶} (\begin{matrix} 8 \\ 16 \end{matrix}) \overset{α^{- 1}}{⟶} (\begin{matrix} 8 \\ 0 \end{matrix})$

Die Verkettung von Abbildung und Umkehrabbildung muss also folgende Bedingung erfüllen:

$α^{- 1} \circ α : (\begin{matrix} x_{1} \\ x_{2} \end{matrix}) \to (\begin{matrix} x_{1} \\ x_{2} \end{matrix})$ bzw. $α^{- 1} \circ α : (\begin{matrix} x_{1}^{'} \\ x_{2}^{'} \end{matrix}) = (\begin{matrix} x_{1} \\ x_{2} \end{matrix})$

Die Verkettung $α^{- 1} \circ α$ von Abbildung und Umkehrabbildung ergibt die identische Abbildung, die jeden Vektor auf sich selbst abbildet.

Bestimmung der Umkehrabbildung einer linearen Abbildung mit Hilfe von Zuordnungen

Wir verdeutlichen die Vorgehensweise für die lineare Abbildung aus Beispiel 1 oben.

Geg.: $α : (\begin{matrix} x_{1}^{'} \\ x_{2}^{'} \end{matrix}) = (\begin{matrix} 1 & - 2 \\ 2 & 1 \end{matrix}) \cdot (\begin{matrix} x_{1} \\ x_{2} \end{matrix})$

Ges.: $α^{- 1} : (\begin{matrix} x_{1}^{'} \\ x_{2}^{'} \end{matrix}) = \dots$ , so dass $α^{- 1} \circ α : (\begin{matrix} x_{1}^{'} \\ x_{2}^{'} \end{matrix}) = (\begin{matrix} x_{1} \\ x_{2} \end{matrix})$ gilt

Der folgende Ansatz geht davon aus, dass $α^{- 1}$ ebenfalls eine lineare Abbildung ist.

$α^{- 1} : (\begin{matrix} x_{1}^{'} \\ x_{2}^{'} \end{matrix}) = (\begin{matrix} a & b \\ c & d \end{matrix}) \cdot (\begin{matrix} x_{1} \\ x_{2} \end{matrix})$

Mit Hilfe vorgegebener Zuordnungen kann man ein lineares Gleichungssystem für die Unbekannten $a$ , $b$ , $c$ , $d$ bestimmen.

Bedingungen	Vektorgleichungen	Koordinatengleichungen
$α^{- 1} : (\begin{matrix} 8 \\ 16 \end{matrix}) \to (\begin{matrix} 8 \\ 0 \end{matrix})$	$(\begin{matrix} a & b \\ c & d \end{matrix}) \cdot (\begin{matrix} 8 \\ 16 \end{matrix}) = (\begin{matrix} 8 \\ 0 \end{matrix})$	$\begin{array}{lrcrcrcr} [1] & 8 a & + & 16 b & = & 8 \\ [2] & 8 c & + & 16 d & = & 0 \end{array}$
$α^{- 1} : (\begin{matrix} - 16 \\ 8 \end{matrix}) \to (\begin{matrix} 0 \\ 8 \end{matrix})$	$(\begin{matrix} a & b \\ c & d \end{matrix}) \cdot (\begin{matrix} - 16 \\ 8 \end{matrix}) = (\begin{matrix} 0 \\ 8 \end{matrix})$	$\begin{array}{lrcrcrcr} [3] & - 16 a & + & 8 b & = & 0 \\ [4] & - 16 c & + & 8 d & = & 8 \end{array}$

Das entstehende lineare Gleichungssystem lässt sich in zwei separate Gleichungssysteme aufteilen und dann mit geeigneten Verfahren lösen. Im vorliegenden Fall erhält man $a = 0.2$ ; $b = 0.4$ ; $c = - 0.4$ ; $d = 0.2$ und somit:

$α^{- 1} : (\begin{matrix} x_{1}^{'} \\ x_{2}^{'} \end{matrix}) = (\begin{matrix} 0.2 & 0.4 \\ - 0.4 & 0.2 \end{matrix}) \cdot (\begin{matrix} x_{1} \\ x_{2} \end{matrix})$

Diese Abbildung $α^{- 1}$ erfüllt die beiden Bedingungen $α^{- 1} : (\begin{matrix} 8 \\ 16 \end{matrix}) \to (\begin{matrix} 8 \\ 0 \end{matrix})$ und $α^{- 1} : (\begin{matrix} - 16 \\ 8 \end{matrix}) \to (\begin{matrix} 0 \\ 8 \end{matrix})$ . Zu klären ist noch, ob sie auch die Bedingung $α^{- 1} \circ α : (\begin{matrix} x_{1}^{'} \\ x_{2}^{'} \end{matrix}) = (\begin{matrix} x_{1} \\ x_{2} \end{matrix})$ erfüllt.

Wir bestimmen $α^{- 1} \circ α$ :

$α^{- 1} \circ α : (\begin{matrix} x_{1}^{'} \\ x_{2}^{'} \end{matrix}) = [(\begin{matrix} 0.2 & 0.4 \\ - 0.4 & 0.2 \end{matrix}) \cdot (\begin{matrix} 1 & - 2 \\ 2 & 1 \end{matrix})] \cdot (\begin{matrix} x_{1} \\ x_{2} \end{matrix}) = (\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}) \cdot (\begin{matrix} x_{1} \\ x_{2} \end{matrix}) = (\begin{matrix} x_{1} \\ x_{2} \end{matrix})$

Beachte: Bei der Umformung verwenden wir folgenden Zusammenhang: Die Abbildungsmatrix $(\begin{matrix} 0.2 & 0.4 \\ - 0.4 & 0.2 \end{matrix})$ ist die inverse Matrix zur Abbildungsmatrix $(\begin{matrix} 1 & - 2 \\ 2 & 1 \end{matrix})$ . Das Produkt der beiden Matrizen liefert die Einheitsmatrix $(\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix})$ .

Wir erhalten folgendes Ergebnis: Die Verkettung $α^{- 1} \circ α$ liefert die identische Abbildung. Die ermittelte Abbildung $α^{- 1}$ ist somit tatsächlich die Umkehrabbildung von $α$ .

Bestimmung der Umkehrabbildung einer linearen Abbildung mit Hilfe der inversen Matrix

Die inverse Matrix $A^{- 1}$ zu einer Matrix $A$ ist die Matrix mit $A^{- 1} \cdot A = E$ . Das Produkt aus der Matrix $A$ und der zugehörigen inversen Matrix $A^{- 1}$ ergibt die (zur Dimension passende) Einheitsmatrix $E$ .

Wenn man die inverse Matrix $A^{- 1}$ zur Abbildungsmatrix $A$ einer linearen Abbildung kennt, dann liefert diese inverse Matrix direkt die Umkehrabbildung. Man kann so argumentieren:

Betrachte eine lineare Abbildung $α : {\vec{x}}^{'} = A \cdot \vec{x}$ mit einer umkehrbaren Abbildungsmatrix $A$ . Für die Abbildung $β : {\vec{x}}^{'} = A^{- 1} \cdot \vec{x}$ gilt dann:

$β \circ α : {\vec{x}}^{'} = A^{- 1} \cdot (A \cdot \vec{x}) = (A^{- 1} \cdot A) \cdot \vec{x} = E \cdot \vec{x} = \vec{x}$

Die Abbildung $β : {\vec{x}}^{'} = A^{- 1} \cdot \vec{x}$ ist somit die Umkehrabbildung zur linearen Abbildung $α : {\vec{x}}^{'} = A \cdot \vec{x}$ . Es gilt also:

$α^{- 1} : {\vec{x}}^{'} = A^{- 1} \cdot \vec{x}$

Die Verwendung der inversen Matrix bei der Bestimmung einer Umkehrabbildung ist dann von besonderem Interesse, wenn man die inverse Matrix zu einer Ausgangsmatrix direkt bestimmen kann – z.B. mit einem Computeralgebrasystem oder mit dem folgenden Satz (aus Kapitel ...).

Eine $2 \times 2$ -Matrix $A = (\begin{matrix} a & b \\ c & d \end{matrix})$ ist genau dann invertierbar, wenn die Bedingung $a d - b c \neq 0$ erfüllt ist. Für die inverse Matrix $A^{- 1}$ gilt dann:

$A^{- 1} = \frac{1}{a d - b c} (\begin{matrix} d & - b \\ - c & a \end{matrix})$

Wir verwenden diesen Satz, um die Umkehrabbildung zur Abbildung aus Beispiel 1 erneut zu bestimmen.

Geg.: $α : (\begin{matrix} x_{1}^{'} \\ x_{2}^{'} \end{matrix}) = (\begin{matrix} 1 & - 2 \\ 2 & 1 \end{matrix}) \cdot (\begin{matrix} x_{1} \\ x_{2} \end{matrix})$

Wir bestimmen die inverse Matrix zur Abbildungsmatrix $A = (\begin{matrix} 1 & - 2 \\ 2 & 1 \end{matrix})$ :

$A^{- 1} = \frac{1}{1 \cdot 1 - (- 2) \cdot 2} (\begin{matrix} 1 & 2 \\ - 2 & 1 \end{matrix}) = \frac{1}{5} (\begin{matrix} 1 & 2 \\ - 2 & 1 \end{matrix}) = (\begin{matrix} 0.2 & 0.4 \\ - 0.4 & 0.2 \end{matrix})$

Es gilt also:

$α^{- 1} : (\begin{matrix} x_{1}^{'} \\ x_{2}^{'} \end{matrix}) = (\begin{matrix} 0.2 & 0.4 \\ - 0.4 & 0.2 \end{matrix}) \cdot (\begin{matrix} x_{1} \\ x_{2} \end{matrix})$

Zusammenfassung - Umkehrabbildung einer linearen Abbildung

Die (teils exemplarisch durchgeführten) durchgeführten Überlegungen lassen sich wie folgt verallgemeinern.

Umkehrabbildung einer affinen Abbildung

Eine lineare Abbildung $α : {\vec{x}}^{'} = A \cdot \vec{x}$ ist genau dann umkehrbar, wenn die Abbildungsmatrix $A$ invertierbar ist. Das ist genau dann der Fall, wenn die Spaltenvektoren der Abbildungsmatrix $A$ linear unabhängig (d.h. keine Vielfache voneinander) sind.

Die Umkehrabbildung $α^{- 1}$ zur Abbildung $α$ erhält man mit der inversen Matrix $A^{- 1}$ .

$α^{- 1} : {\vec{x}}^{'} = A^{- 1} \cdot \vec{x}$

Die Umkehrabbildung $α^{- 1}$ zur linearen Abbildung $α$ ist ebenfalls eine lineare Abbildung.

Bestimmung der Umkehrabbildung einer affinen Abbildung mit Hilfe der inversen Matrix

Wir starten mit einem Beispiel:

Geg.: $α : (\begin{matrix} x_{1}^{'} \\ x_{2}^{'} \end{matrix}) = (\begin{matrix} 1 & - 2 \\ 2 & 1 \end{matrix}) \cdot (\begin{matrix} x_{1} \\ x_{2} \end{matrix}) + (\begin{matrix} - 8 \\ - 4 \end{matrix})$

Beachte, dass die affine Abbildung im Beispiel hier aus der linearen Abbildung im Beispiel oben durch Hinzufügen eines Verschiebevektors hervorgeht. Im vorliegenden Fall ist es daher günstig, die Abbildung $α$ in zwei Teilabbildungen $α_{1}$ und $α_{2}$ aufzuteilen:

$α_{1} : (\begin{matrix} x_{1}^{'} \\ x_{2}^{'} \end{matrix}) = (\begin{matrix} 1 & - 2 \\ 2 & 1 \end{matrix}) \cdot (\begin{matrix} x_{1} \\ x_{2} \end{matrix})$

$α_{2} : (\begin{matrix} x_{1}^{'} \\ x_{2}^{'} \end{matrix}) = (\begin{matrix} x_{1} \\ x_{2} \end{matrix}) + (\begin{matrix} - 8 \\ - 4 \end{matrix})$

Diese Aufteilung ist günstig, weil man die Umkehrabbildung $α_{1}^{- 1}$ bereits kennt und die Umkehrabbildung $α_{2}^{- 1}$ direkt angeben kann:

$α_{1}^{- 1} : (\begin{matrix} x_{1}^{'} \\ x_{2}^{'} \end{matrix}) = (\begin{matrix} 0.2 & 0.4 \\ - 0.4 & 0.2 \end{matrix}) \cdot (\begin{matrix} x_{1} \\ x_{2} \end{matrix})$

$α_{2}^{- 1} : (\begin{matrix} x_{1}^{'} \\ x_{2}^{'} \end{matrix}) = (\begin{matrix} x_{1} \\ x_{2} \end{matrix}) - (\begin{matrix} - 8 \\ - 4 \end{matrix})$

Abbildung	Umkehrabbildung

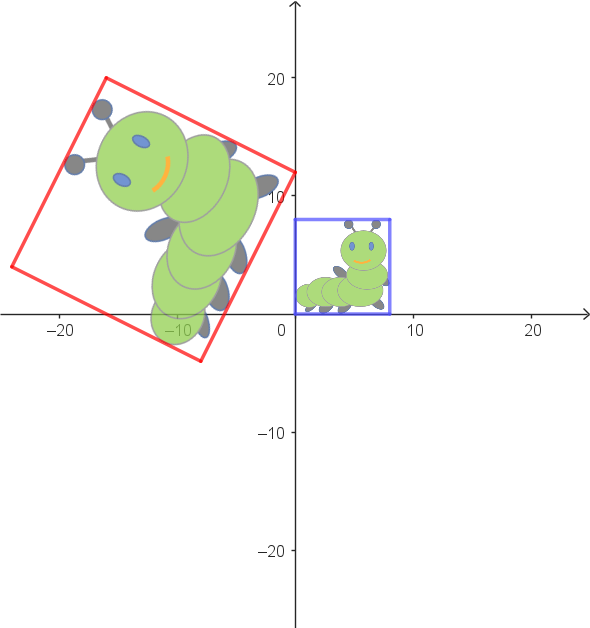
Zuordnungsbeispiel: $α : (\begin{matrix} 8 \\ 0 \end{matrix}) \overset{α_{1}}{⟶} (\begin{matrix} 8 \\ 16 \end{matrix}) \overset{α_{2}}{⟶} (\begin{matrix} 0 \\ 12 \end{matrix})$	Zuordnungsbeispiele: $α^{- 1} : (\begin{matrix} 0 \\ 12 \end{matrix}) \overset{α_{2}^{- 1}}{⟶} (\begin{matrix} 8 \\ 16 \end{matrix}) \overset{α_{1}^{- 1}}{⟶} (\begin{matrix} 8 \\ 0 \end{matrix})$
Vektorgleichung als allgemeine Zuordnungsvorschrift: $\begin{array}{llll} α : & (\begin{array}{c} x_{1} \\ x_{2} \end{array}) \\ ↓ α_{1} \\ (\begin{array}{c} 1 & - 2 \\ 2 & 1 \end{array}) \cdot (\begin{array}{c} x_{1} \\ x_{2} \end{array}) \\ ↓ α_{2} \\ (\begin{array}{c} 1 & - 2 \\ 2 & 1 \end{array}) \cdot (\begin{array}{c} x_{1} \\ x_{2} \end{array}) + (\begin{array}{c} - 8 \\ - 4 \end{array}) \end{array}$	Vektorgleichung als allgemeine Zuordnungsvorschrift: $\begin{array}{llll} α^{- 1} : & (\begin{array}{c} x_{1} \\ x_{2} \end{array}) \\ ↓ α_{2}^{- 1} \\ (\begin{array}{c} x_{1} \\ x_{2} \end{array}) - (\begin{array}{c} - 8 \\ - 4 \end{array}) \\ ↓ α_{1}^{- 1} \\ (\begin{array}{c} 0.2 & 0.4 \\ - 0.4 & 0.2 \end{array}) \cdot [(\begin{array}{c} x_{1} \\ x_{2} \end{array}) - (\begin{array}{c} - 8 \\ - 4 \end{array})] \end{array}$

Durch Umformen der Vektorgleichung erhält man folgende algebraische Darstellung von $α^{- 1}$ :

$\begin{array}{llll} α^{- 1} : (\begin{array}{c} x_{1}^{'} \\ x_{2}^{'} \end{array}) & = & (\begin{array}{c} 0.2 & 0.4 \\ - 0.4 & 0.2 \end{array}) \cdot [(\begin{array}{c} x_{1} \\ x_{2} \end{array}) - (\begin{array}{c} - 8 \\ - 4 \end{array})] \\ = & (\begin{array}{c} 0.2 & 0.4 \\ - 0.4 & 0.2 \end{array}) \cdot (\begin{array}{c} x_{1} \\ x_{2} \end{array}) - (\begin{array}{c} 0.2 & 0.4 \\ - 0.4 & 0.2 \end{array}) \cdot (\begin{array}{c} - 8 \\ - 4 \end{array}) \\ = & (\begin{array}{c} 0.2 & 0.4 \\ - 0.4 & 0.2 \end{array}) \cdot (\begin{array}{c} x_{1} \\ x_{2} \end{array}) - (\begin{array}{c} - 3.2 \\ 2.4 \end{array}) \\ = & (\begin{array}{c} 0.2 & 0.4 \\ - 0.4 & 0.2 \end{array}) \cdot (\begin{array}{c} x_{1} \\ x_{2} \end{array}) + (\begin{array}{c} 3.2 \\ - 2.4 \end{array}) \end{array}$

Die Überlegungen im Beispiel lassen sich direkt verallgemein. Betrachte eine affine Abbildung $α : {\vec{x}}^{'} = A \cdot \vec{x} + \vec{v}$ mit einer umkehrbaren Abbildungsmatrix $A$ . Auch hier zerlegen wir $α$ in zwei Teilabbildungen $α_{1}$ und $α_{2}$ :

$α : \vec{x} \overset{α_{1}}{⟶} A \cdot \vec{x} \overset{α_{2}}{⟶} A \cdot \vec{x} + \vec{v}$

Für $α^{- 1}$ gilt dann:

$α^{- 1} : \vec{x} \overset{α_{2}^{- 1}}{⟶} \vec{x} - \vec{v} \overset{α_{1}^{- 1}}{⟶} A^{- 1} \cdot (\vec{x} - \vec{v})$

Eine Umformung zeigt dann, dass $α^{- 1}$ ebenfalls eine affine Abbildung ist.

$α^{- 1} : {\vec{x}}^{'} = A^{- 1} \cdot (\vec{x} - \vec{v}) = A^{- 1} \cdot \vec{x} - A^{- 1} \cdot \vec{v} = A^{- 1} \cdot \vec{x} + (- A^{- 1} \cdot \vec{v})$

Wir fassen das Ergebnis im folgenden Satz zusammen.

Umkehrabbildung einer affinen Abbildung

Eine affine Abbildung $α : {\vec{x}}^{'} = A \cdot \vec{x} + \vec{v}$ ist genau dann umkehrbar, wenn die Abbildungsmatrix $A$ invertierbar ist. Die Umkehrabbildung $α^{- 1}$ zur Abbildung $α$ erhält man mit der inversen Matrix $A^{- 1}$ .

$α^{- 1} : {\vec{x}}^{'} = A^{- 1} \cdot (\vec{x} - \vec{v}) = A^{- 1} \cdot \vec{x} + (- A^{- 1} \cdot \vec{v})$

Die Umkehrabbildung $α^{- 1}$ zur affinen Abbildung $α$ ist ebenfalls eine affine Abbildung.

Zusammenfassung - Umkehrung affiner Abbildungen

Die Grundidee

Beispiel 1: umkehrbare Abbildung

Beispiel 2: nicht umkehrbare Abbildung

Beschreibung mit Fachbegriffen

Umkehrabbildung

Bestimmung der Umkehrabbildung einer linearen Abbildung mit Hilfe von Zuordnungen

Bestimmung der Umkehrabbildung einer linearen Abbildung mit Hilfe der inversen Matrix

Zusammenfassung - Umkehrabbildung einer linearen Abbildung

Umkehrabbildung einer affinen Abbildung

Bestimmung der Umkehrabbildung einer affinen Abbildung mit Hilfe der inversen Matrix

Umkehrabbildung einer affinen Abbildung

Suche

Rückmeldung geben