Vertiefung

Ein Beispiel betrachten

Die Gerade $x=2$ ist die Menge aller Punkte mit $x$-Koordinate $2$ – also die Parallele zur $y$-Achse, die durch $(2|0)$ verläuft. Entsprechend ist die Gerade $x=5$ die Parallele zur $y$-Achse, die durch $(5|0)$ verläuft.

Aufgabe 1

Führe die Verkettungen $\beta \circ \alpha$ und $\alpha \circ \beta$ per Hand mit einer selbst gewählten Figur durch. Stelle Vermutungen darüber auf, was die Abbildungen $\beta \circ \alpha$ und die $\alpha \circ \beta$ leisten.

Aufgabe 2

In der folgenden Übersicht wird die Abbildung $\beta \circ \alpha$: Spiegelung an der Geraden $x=5$ nach Spiegelung an der Geraden $x=2$ verdeutlicht.

Teilabbildung 1	Teilabbildung 2
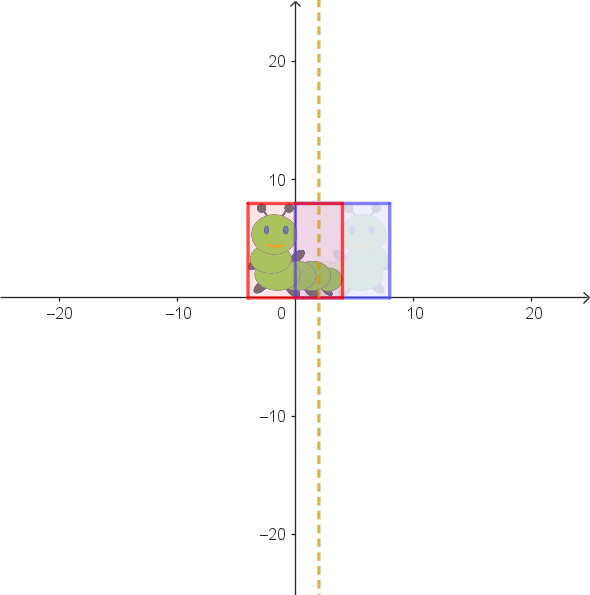
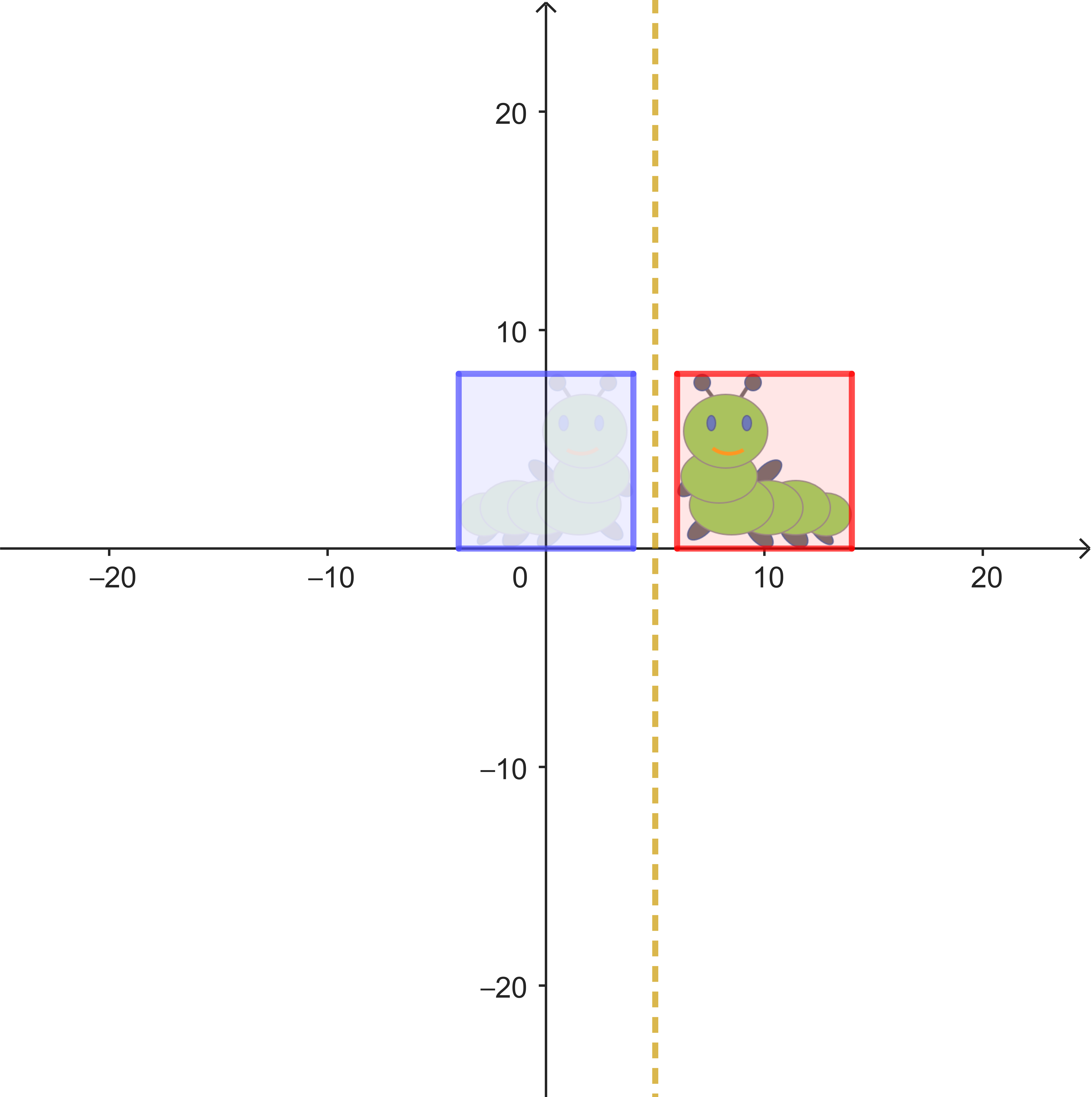
Spiegelung an der Geraden $x=2$	Spiegelung an der Geraden $x=5$
$\alpha :\left(\begin{array}{c}{x}_1^{\prime }\\ x_2^{\prime }\end{array}\right)=\left(\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right)\cdot \left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)+\left(\begin{array}{c}4\\ 0\end{array}\right)$	$\beta :\left(\begin{array}{c}{x}_1^{\prime }\\ x_2^{\prime }\end{array}\right)=\left(\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right)\cdot \left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)+\left(\begin{array}{c}10\\ 0\end{array}\right)$

(a) Zeige, dass die Abbildung $\beta \circ \alpha$ so beschrieben werden kann:

$\beta \circ \alpha :\left(\begin{array}{c}{x}_1^{\prime }\\ x_2^{\prime }\end{array}\right)=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)\cdot \left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)+\left(\begin{array}{c}6\\ 0\end{array}\right)=\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)+\left(\begin{array}{c}6\\ 0\end{array}\right)$

Hilfe

Es gilt:

$\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)\stackrel{\alpha }{⟶}\left(\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right)\cdot \left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)+\left(\begin{array}{c}4\\ 0\end{array}\right)\stackrel{\beta }{⟶}\left(\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right)\cdot [\left(\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right)\cdot \left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)+\left(\begin{array}{c}4\\ 0\end{array}\right)]+\left(\begin{array}{c}10\\ 0\end{array}\right)$

Hilfe

Durch Umformen erhält man:

$\begin{array}{l}\left(\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right)\cdot [\left(\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right)\cdot \left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)+\left(\begin{array}{c}4\\ 0\end{array}\right)]+\left(\begin{array}{c}10\\ 0\end{array}\right)=\dots \end{array}$

(b) Begründe: Die Abbildung $\beta \circ \alpha$ entspricht einer Verschiebung um $6$ Einheiten in $x$-Richtung.

Aufgabe 3

Betrachte die Verkettung $\alpha \circ \beta$: Spiegelung an der Geraden $x=2$ nach Spiegelung an der Geraden $x=5$. Kläre folgende Frage: Entspricht diese Abbildung ebenfalls einer Verschiebung?

Ergebnisse verallgemeinern

Aufgabe 4

Betrachte die Verkettung $\beta \circ \alpha$ von zwei affinen Abbildungen $\alpha :{\overrightarrow{x}}^{\prime }=A\cdot \overrightarrow{x}+\overrightarrow{v}$ und $\beta :{\overrightarrow{x}}^{\prime }=B\cdot \overrightarrow{x}+\overrightarrow{w}$.

(a) Ergänze die algebraische Beschreibung von $\beta \circ \alpha$:

$\beta \circ \alpha :{\overrightarrow{x}}^{\prime }=\dots$

(b) Ist die Verkettung $\beta \circ \alpha$ ebenfalls eine affine Abbildung? Begründe.

Aufgabe 5

Schaue dir nochmal das Beispiel oben an. Darf man die Reihenfolge bei der Verkettung von affinen Abbildungen vertauschen bzw. gilt $\beta \circ \alpha =\alpha \circ \beta$ bei beliebigen affinen Abbildungen?

Aufgabe 6

Sichere deine Ergebnisse.

Beachte: Die Verkettung von (affinen) Abbildungen ist nicht kommutativ.