o-mathe | Einstieg » Erarbeitung

Erarbeitung

Zur Orientierung

Hier geht es darum, das Umkehren von linearen Abbildungen algebraisch durchzuführen.

Ein Beispiel analysieren

Wir starten mit dem Beispiel aus dem Erkundungskapitel.

Abbildung	Umkehrabbildung

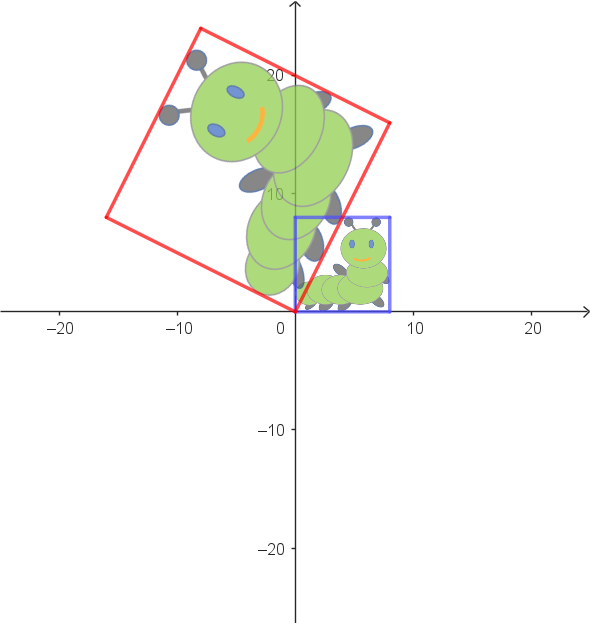
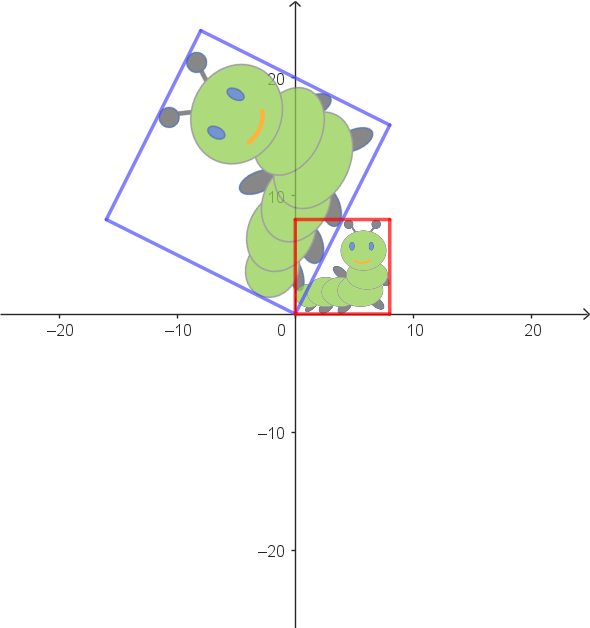
Zuordnungsbeispiele: $α : (\begin{matrix} 8 \\ 0 \end{matrix}) \to (\begin{matrix} 8 \\ 16 \end{matrix})$ $α : (\begin{matrix} 0 \\ 8 \end{matrix}) \to (\begin{matrix} - 16 \\ 8 \end{matrix})$	Zuordnungsbeispiele: $α^{- 1} : (\begin{matrix} 8 \\ 16 \end{matrix}) \to (\begin{matrix} 8 \\ 0 \end{matrix})$ $α^{- 1} : (\begin{matrix} - 16 \\ 8 \end{matrix}) \to (\begin{matrix} 0 \\ 8 \end{matrix})$
Vektorgleichung als allgemeine Zuordnungsvorschrift: $α : (\begin{matrix} x_{1}^{'} \\ x_{2}^{'} \end{matrix}) = (\begin{matrix} 1 & - 2 \\ 2 & 1 \end{matrix}) \cdot (\begin{matrix} x_{1} \\ x_{2} \end{matrix})$	Vektorgleichung als allgemeine Zuordnungsvorschrift: $α^{- 1} : (\begin{matrix} x_{1}^{'} \\ x_{2}^{'} \end{matrix}) = (\begin{matrix} 0.2 & 0.4 \\ - 0.4 & 0.2 \end{matrix}) \cdot (\begin{matrix} x_{1} \\ x_{2} \end{matrix})$

Im Erkundungskapitel wurde im Beispiel oben die Umkehrabbildung ausgehend von den gezeigten Zuordnungsbeispiele (zur Umkehrabbildung) bestimmt. Wir schauen uns jetzt die erzielte Matrix $B = (\begin{matrix} 0.2 & 0.4 \\ - 0.4 & 0.2 \end{matrix})$ genauer an. Hierzu benötigen wir das Konzept der inversen Matrix.

Wiederholung

Die inverse Matrix $A^{- 1}$ zu einer Matrix $A$ ist die Matrix mit $A^{- 1} \cdot A = E$ und $A \cdot A^{- 1} = E$ . Das Produkt aus der Matrix $A$ und der zugehörigen inversen Matrix $A^{- 1}$ ergibt die (zur Dimension passende) Einheitsmatrix $E$ .

Aufgabe 1

(a) Zeige, dass die Matrix $B = (\begin{matrix} 0.2 & 0.4 \\ - 0.4 & 0.2 \end{matrix})$ die inverse Matrix zur Abbildungsmatrix $A = (\begin{matrix} 1 & - 2 \\ 2 & 1 \end{matrix})$ ist. Berechne hierzu das folgende Matrixprodukt:

$\underset{B}{\underset{⏟}{(\begin{matrix} 0.2 & 0.4 \\ - 0.4 & 0.2 \end{matrix})}} \cdot \underset{A}{\underset{⏟}{(\begin{matrix} 1 & - 2 \\ 2 & 1 \end{matrix})}} = \dots$

(b) Zeige mit Hilfe von (a), dass die Abbildung $α^{- 1} : (\begin{matrix} x_{1}^{'} \\ x_{2}^{'} \end{matrix}) = (\begin{matrix} 0.2 & 0.4 \\ - 0.4 & 0.2 \end{matrix}) \cdot (\begin{matrix} x_{1} \\ x_{2} \end{matrix})$ die Umkehrabbildung zur Abbildung $α : (\begin{matrix} x_{1}^{'} \\ x_{2}^{'} \end{matrix}) = (\begin{matrix} 1 & - 2 \\ 2 & 1 \end{matrix}) \cdot (\begin{matrix} x_{1} \\ x_{2} \end{matrix})$ ist. Ergänze hierzu die fehlenden Berechnungen.

$α^{- 1} \circ α : (\begin{matrix} x_{1}^{'} \\ x_{2}^{'} \end{matrix}) = (\begin{matrix} 0.2 & 0.4 \\ - 0.4 & 0.2 \end{matrix}) \cdot [(\begin{matrix} 1 & - 2 \\ 2 & 1 \end{matrix}) \cdot (\begin{matrix} x_{1} \\ x_{2} \end{matrix})] = \dots$

Überlegungen verallgemeinern

Die am Beispiel exemplarisch durchgeführten Überlegungen lassen sich wie folgt verallgemeinern.

Umkehrabbildung einer linearen Abbildung

(a) Wenn die lineare Abbildung $α : {\vec{x}}^{'} = A \cdot \vec{x}$ umkehrbar ist, dann ist die Matrix $A$ invertierbar und es gilt:

$α^{- 1} : {\vec{x}}^{'} = A^{- 1} \cdot \vec{x}$

(b) Wenn die Matrix $A$ invertierbar ist, dann ist die lineare Abbildung $α : {\vec{x}}^{'} = A \cdot \vec{x}$ umkehrbar und es gilt:

$α^{- 1} : {\vec{x}}^{'} = A^{- 1} \cdot \vec{x}$

(c) Die Umkehrabbildung einer umkehrbaren linearen Abbildung ist ebenfalls eine lineare Abbildung.

Aufgabe 2

Verdeutliche anhand des folgenden Beispiels: Wenn man inverse Matrizen bestimmen kann, dann kann man auch Umkehrabbildungen von linearen Abbildungen bestimmen.

(a) Zeige, dass die Matrix $(\begin{matrix} \frac{1}{3} & - \frac{2}{3} \\ \frac{2}{3} & - \frac{1}{3} \end{matrix})$ die inverse Matrix zur Matrix $(\begin{matrix} - 1 & 2 \\ - 2 & 1 \end{matrix})$ ist.

(b) Bestimme die Umkehrabbildung zur linearen Abbildung $α : (\begin{matrix} x_{1}^{'} \\ x_{2}^{'} \end{matrix}) = (\begin{matrix} - 1 & 2 \\ - 2 & 1 \end{matrix}) \cdot (\begin{matrix} x_{1} \\ x_{2} \end{matrix})$ .

←Zurück Weiter→