Vertiefung

Ein Beispiel analysieren

Wir starten mit dem Beispiel aus dem Erkundungskapitel.

$\alpha :\left(\begin{array}{c}{x}_1^{\prime }\\ x_2^{\prime }\end{array}\right)=\left(\begin{array}{cc}1& -2\\ 2& 1\end{array}\right)\cdot \left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)+\left(\begin{array}{c}-8\\ -4\end{array}\right)$

Ziel ist es, für diese Abbildung die Umkehrabbildung zu ermitteln.

Im vorliegenden Fall ist es günstig, die Abbildung $\alpha$ in zwei Teilabbildungen ${\alpha }_1$ und ${\alpha }_2$ aufzuteilen:

${\alpha }_1:\left(\begin{array}{c}{x}_1^{\prime }\\ x_2^{\prime }\end{array}\right)=\left(\begin{array}{cc}1& -2\\ 2& 1\end{array}\right)\cdot \left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)$

${\alpha }_2:\left(\begin{array}{c}{x}_1^{\prime }\\ x_2^{\prime }\end{array}\right)=\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)+\left(\begin{array}{c}-8\\ -4\end{array}\right)$

Diese Aufteilung ist günstig, weil man die Umkehrabbildung ${\alpha }_1^{-1}$ bereits kennt und die Umkehrabbildung ${\alpha }_2^{-1}$ direkt angeben kann:

${\alpha }_1^{-1}:\left(\begin{array}{c}{x}_1^{\prime }\\ x_2^{\prime }\end{array}\right)=\left(\begin{array}{cc}0.2& 0.4\\ -0.4& 0.2\end{array}\right)\cdot \left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)$

${\alpha }_2^{-1}:\left(\begin{array}{c}{x}_1^{\prime }\\ x_2^{\prime }\end{array}\right)=\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)-\left(\begin{array}{c}-8\\ -4\end{array}\right)$

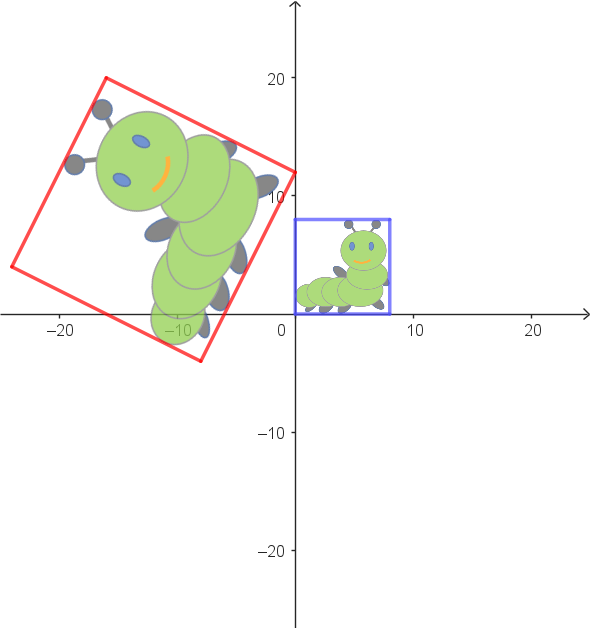
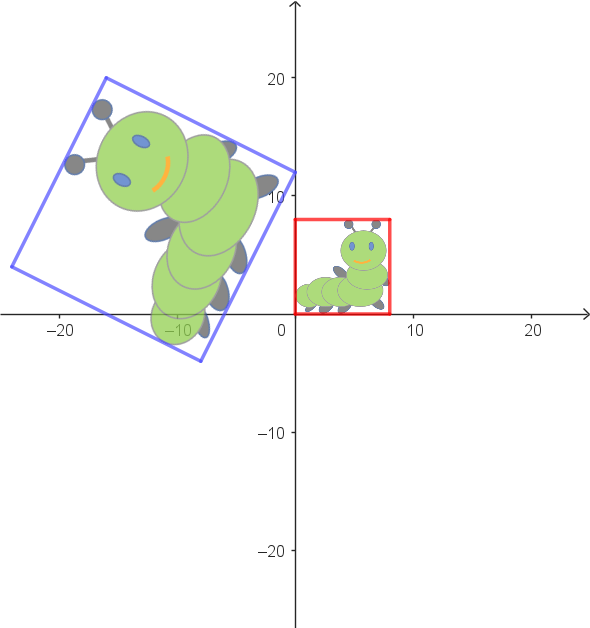
Abbildung	Umkehrabbildung
Zuordnungsbeispiel: $\alpha :\left(\begin{array}{c}8\\ 0\end{array}\right)\stackrel{{\alpha }_1}{⟶}\left(\begin{array}{c}8\\ 16\end{array}\right)\stackrel{{\alpha }_2}{⟶}\left(\begin{array}{c}0\\ 12\end{array}\right)$	Zuordnungsbeispiele: ${\alpha }^{-1}:\left(\begin{array}{c}0\\ 12\end{array}\right)\stackrel{{\alpha }_2^{-1}}{⟶}\left(\begin{array}{c}8\\ 16\end{array}\right)\stackrel{{\alpha }_1^{-1}}{⟶}\left(\begin{array}{c}8\\ 0\end{array}\right)$
Vektorgleichung als allgemeine Zuordnungsvorschrift: $\begin{array}{ll}\alpha :& \left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)\\ & \downarrow {\alpha }_1\\ & \left(\begin{array}{cc}1& -2\\ 2& 1\end{array}\right)\cdot \left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)\\ & \downarrow {\alpha }_2\\ & \left(\begin{array}{cc}1& -2\\ 2& 1\end{array}\right)\cdot \left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)+\left(\begin{array}{c}-8\\ -4\end{array}\right)\end{array}$	Vektorgleichung als allgemeine Zuordnungsvorschrift: $\begin{array}{ll}{\alpha }^{-1}:& \left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)\\ & \downarrow {\alpha }_2^{-1}\\ & \left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)-\left(\begin{array}{c}-8\\ -4\end{array}\right)\\ & \downarrow {\alpha }_1^{-1}\\ & \left(\begin{array}{cc}0.2& 0.4\\ -0.4& 0.2\end{array}\right)\cdot [\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)-\left(\begin{array}{c}-8\\ -4\end{array}\right)]\end{array}$

Durch Umformen der Vektorgleichung erhält man folgende algebraische Darstellung von ${\alpha }^{-1}$:

$\begin{array}{lll}{\alpha }^{-1}:\left(\begin{array}{c}{x}_1^{\prime }\\ x_2^{\prime }\end{array}\right)& =& \left(\begin{array}{cc}0.2& 0.4\\ -0.4& 0.2\end{array}\right)\cdot [\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)-\left(\begin{array}{c}-8\\ -4\end{array}\right)]\\ & =& \left(\begin{array}{cc}0.2& 0.4\\ -0.4& 0.2\end{array}\right)\cdot \left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)-\left(\begin{array}{cc}0.2& 0.4\\ -0.4& 0.2\end{array}\right)\cdot \left(\begin{array}{c}-8\\ -4\end{array}\right)\\ & =& \left(\begin{array}{cc}0.2& 0.4\\ -0.4& 0.2\end{array}\right)\cdot \left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)-\left(\begin{array}{c}-3.2\\ 2.4\end{array}\right)\\ & =& \left(\begin{array}{cc}0.2& 0.4\\ -0.4& 0.2\end{array}\right)\cdot \left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)+\left(\begin{array}{c}3.2\\ -2.4\end{array}\right)\end{array}$

Aufgabe 1

Mache dich nochmal mit den Überlegungen im Beispiel vertraut. Erläutere jeden einzelnen Argumentationsschritt.

Überlegungen verallgemeinern

Betrachte eine affine Abbildung $\alpha :{\overrightarrow{x}}^{\prime }=A\cdot \overrightarrow{x}+\overrightarrow{v}$ mit einer umkehrbaren Abbildungsmatrix $A$.

Aufgabe 2

(a) Gehe analog zum Beispiel vor und zerlege $\alpha$ in Teilabbildungen ${\alpha }_1$ und ${\alpha }_2$:

$\alpha :\overrightarrow{x}\stackrel{{\alpha }_1}{⟶}\cdots \stackrel{{\alpha }_2}{⟶}\dots$

(b) Leite analog zum Beispiel oben eine Vektorgleichung für ${\alpha }^{-1}$ her.

${\alpha }^{-1}:\overrightarrow{x}\stackrel{{\alpha }_2^{-1}}{⟶}\cdots \stackrel{{\alpha }_1^{-1}}{⟶}\dots$

(c) Zeige mit einer Umformung, dass ${\alpha }^{-1}$ ebenfalls eine affine Abbildung ist.

Ergebnisse zusammenfassen

Wir fassen das Ergebnis im folgenden Satz zusammen.