o-mathe | Umkehrung affiner Abbildungen » Überprüfung

Überprüfung - Umkehrung von Abbildungen

Aufgabe 1

In der folgenden Übersicht wird die Abbildung $α : (\begin{matrix} x_{1}^{'} \\ x_{2}^{'} \end{matrix}) = (\begin{matrix} 0 & - 2 \\ 2 & 0 \end{matrix}) \cdot (\begin{matrix} x_{1} \\ x_{2} \end{matrix})$ und die zugehörige Umkehrabbildung $α^{- 1}$ exemplarisch verdeutlicht.

Abbildung (blau -> rot)	Umkehrabbildung (blau -> rot)

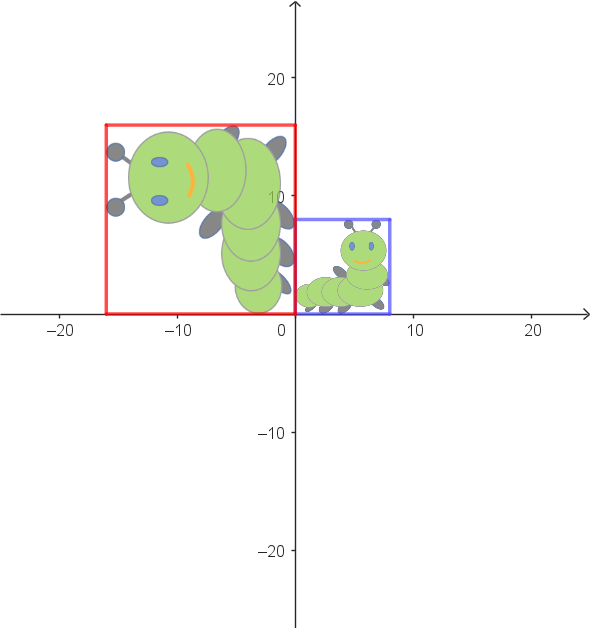
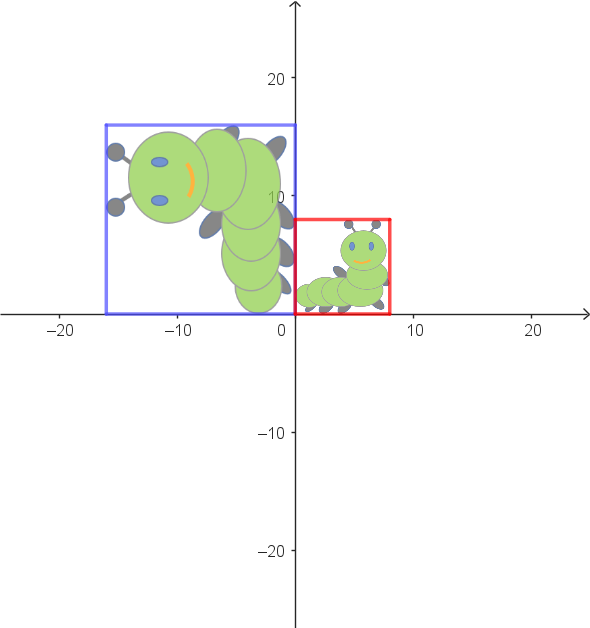
Aufgabe 1

Was bedeutet die Aussage: $α^{- 1}$ ist die Umkehrabbildung zur Abbildung $α$ ? Erkläre das mit Hilfe von Zuordnungen.

Zur Kontrolle

$α^{- 1}$ kehrt die Zuordnungen der Abbildung $α$ alle um.

Beispiel:

$α : (\begin{matrix} 8 \\ 0 \end{matrix}) \to (\begin{matrix} 0 \\ 16 \end{matrix})$
$α^{- 1} : (\begin{matrix} 0 \\ 16 \end{matrix}) \to (\begin{matrix} 8 \\ 0 \end{matrix})$

Aufgabe 2

Wie kann man man $α^{- 1}$ mit Hilfe von Zuordnungen bestimmen? Führe das Verfahren selbst durch.

Zur Kontrolle

Ansatz: $α^{- 1}$ ist ebenfalls eine lineare Abbildung: $α^{- 1} : (\begin{matrix} x_{1}^{'} \\ x_{2}^{'} \end{matrix}) = (\begin{matrix} a & b \\ c & d \end{matrix}) \cdot (\begin{matrix} x_{1} \\ x_{2} \end{matrix})$

Bedingungen	Vektorgleichungen	Koordinatengleichungen	Lösungen
$α^{- 1} : (\begin{matrix} 0 \\ 16 \end{matrix}) \to (\begin{matrix} 8 \\ 0 \end{matrix})$	$(\begin{matrix} a & b \\ c & d \end{matrix}) \cdot (\begin{matrix} 0 \\ 16 \end{matrix}) = (\begin{matrix} 8 \\ 0 \end{matrix})$	$\begin{array}{lrcrcrcr} [1] & 16 b & = & 8 \\ [2] & 16 d & = & 0 \end{array}$	$\begin{array}{lcl} b & = & 0.5 \\ d & = & 0 \end{array}$
$α^{- 1} : (\begin{matrix} - 16 \\ 0 \end{matrix}) \to (\begin{matrix} 0 \\ 8 \end{matrix})$	$(\begin{matrix} a & b \\ c & d \end{matrix}) \cdot (\begin{matrix} - 16 \\ 0 \end{matrix}) = (\begin{matrix} 0 \\ 8 \end{matrix})$	$\begin{array}{lrcrcrcr} [3] & - 16 a & = & 0 \\ [4] & - 16 c & = & 8 \end{array}$	$\begin{array}{lcl} a & = & 0 \\ c & = & - 0.5 \end{array}$

Erbebnis: $α^{- 1} : (\begin{matrix} x_{1}^{'} \\ x_{2}^{'} \end{matrix}) = (\begin{matrix} 0 & 0.5 \\ - 0.5 & 0 \end{matrix}) \cdot (\begin{matrix} x_{1} \\ x_{2} \end{matrix})$

Aufgabe 3

Wie kann man man $α^{- 1}$ mit Hilfe einer inversen Matrix bestimmen? Erläutere das Verfahren.

Zur Kontrolle

Betrachte die Abbildungsmatrix $A = (\begin{matrix} 0 & - 2 \\ 2 & 0 \end{matrix})$ der Abbildung $α$ .

Für die inverse Matrix $A^{- 1}$ gilt: $A^{- 1} = (\begin{matrix} 0 & 0.5 \\ - 0.5 & 0 \end{matrix})$ .

Diese inverse Matrix kann man im vorliegenden Beispiel leicht erschließen. In schwierigeren Fällen kann man die inverse Matrix mit einer Formel oder mit einem Computeralgebrasystem bestimmen.

Also: $α^{- 1} : (\begin{matrix} x_{1}^{'} \\ x_{2}^{'} \end{matrix}) = (\begin{matrix} 0 & 0.5 \\ - 0.5 & 0 \end{matrix}) \cdot (\begin{matrix} x_{1} \\ x_{2} \end{matrix})$

Aufgabe 4

Betrachte die Abbildung $β$ , die $α$ mit einer Verschiebung kombiniert.

$β : (\begin{matrix} x_{1}^{'} \\ x_{2}^{'} \end{matrix}) = (\begin{matrix} 0 & - 2 \\ 2 & 0 \end{matrix}) \cdot (\begin{matrix} x_{1} \\ x_{2} \end{matrix}) + (\begin{matrix} 2 \\ 2 \end{matrix})$

Wie kann man man $β^{- 1}$ mit Hilfe von $α^{- 1}$ bestimmen? Erläutere das Verfahren.

Zur Kontrolle

Mit der Verschiebung $γ : (\begin{matrix} x_{1}^{'} \\ x_{2}^{'} \end{matrix}) = (\begin{matrix} x_{1} \\ x_{2} \end{matrix}) + (\begin{matrix} 2 \\ 2 \end{matrix})$ kann man $β$ auch so darstellen:

$β : (\begin{matrix} x_{1} \\ x_{2} \end{matrix}) \overset{α}{⟶} (\begin{matrix} 0 & - 2 \\ 2 & 0 \end{matrix}) \cdot (\begin{matrix} x_{1} \\ x_{2} \end{matrix}) \overset{γ}{⟶} (\begin{matrix} 0 & - 2 \\ 2 & 0 \end{matrix}) \cdot (\begin{matrix} x_{1} \\ x_{2} \end{matrix}) + (\begin{matrix} 2 \\ 2 \end{matrix})$

Die Umkehrabbildung erhält man dann so:

$β^{- 1} : (\begin{matrix} x_{1} \\ x_{2} \end{matrix}) \overset{γ^{- 1}}{⟶} (\begin{matrix} x_{1} \\ x_{2} \end{matrix}) + (\begin{matrix} - 2 \\ - 2 \end{matrix}) \overset{α^{- 1}}{⟶} (\begin{matrix} 0 & 0.5 \\ - 0.5 & 0 \end{matrix}) \cdot [(\begin{matrix} x_{1} \\ x_{2} \end{matrix}) + (\begin{matrix} - 2 \\ - 2 \end{matrix})] = (\begin{matrix} 0 & 0.5 \\ - 0.5 & 0 \end{matrix}) \cdot (\begin{matrix} x_{1} \\ x_{2} \end{matrix}) + (\begin{matrix} - 1 \\ 1 \end{matrix})$

Also: $β^{- 1} : (\begin{matrix} x_{1}^{'} \\ x_{2}^{'} \end{matrix}) = (\begin{matrix} 0 & 0.5 \\ - 0.5 & 0 \end{matrix}) \cdot (\begin{matrix} x_{1} \\ x_{2} \end{matrix}) + (\begin{matrix} - 1 \\ 1 \end{matrix})$

Überprüfung - Umkehrung von Abbildungen

Aufgabe 1

Aufgabe 1

Aufgabe 2

Aufgabe 3

Aufgabe 4

Suche

Rückmeldung geben