Einstieg
Die Problemsituation klären
Wir starten mit Beispielen aus dem Erkundungskapitel.
Beispiel 1: umkehrbare Abbildung
| Abbildung | Umkehrabbildung |
|---|---|
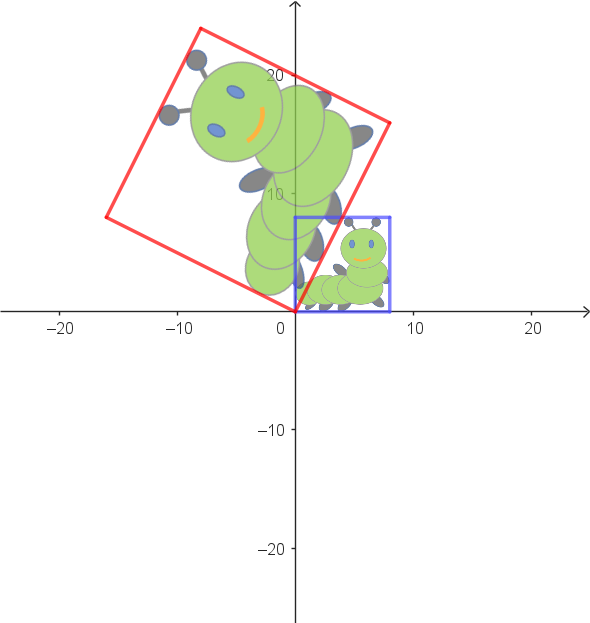
|
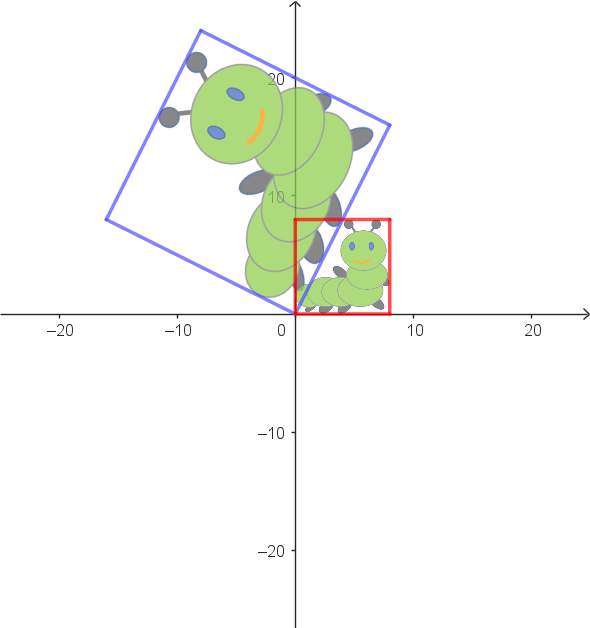
|
|
Zuordnungsbeispiele: $\alpha: \begin{pmatrix} 8 \\ 0 \end{pmatrix} \rightarrow \begin{pmatrix} 8 \\ 16 \end{pmatrix}$ $\alpha: \begin{pmatrix} 0 \\ 8 \end{pmatrix} \rightarrow \begin{pmatrix} -16 \\ 8 \end{pmatrix}$ |
Zuordnungsbeispiele: $\alpha^{-1}: \begin{pmatrix} 8 \\ 16 \end{pmatrix} \rightarrow \begin{pmatrix} 8 \\ 0 \end{pmatrix}$ $\alpha^{-1}: \begin{pmatrix} -16 \\ 8 \end{pmatrix} \rightarrow \begin{pmatrix} 0 \\ 8 \end{pmatrix}$ |
|
Vektorgleichung als allgemeine Zuordnungsvorschrift: $\alpha: \begin{pmatrix} x_1' \\ x_2' \end{pmatrix} = \begin{pmatrix} 1 & -2 \\ 2 & 1 \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}$ |
Vektorgleichung als allgemeine Zuordnungsvorschrift: $\alpha^{-1}: \begin{pmatrix} x_1' \\ x_2' \end{pmatrix} = \begin{pmatrix} 0.2 & 0.4 \\ -0.4 & 0.2 \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}$ |
Beispiel 2: nicht umkehrbare Abbildung
| Abbildung | Umkehrabbildung |
|---|---|
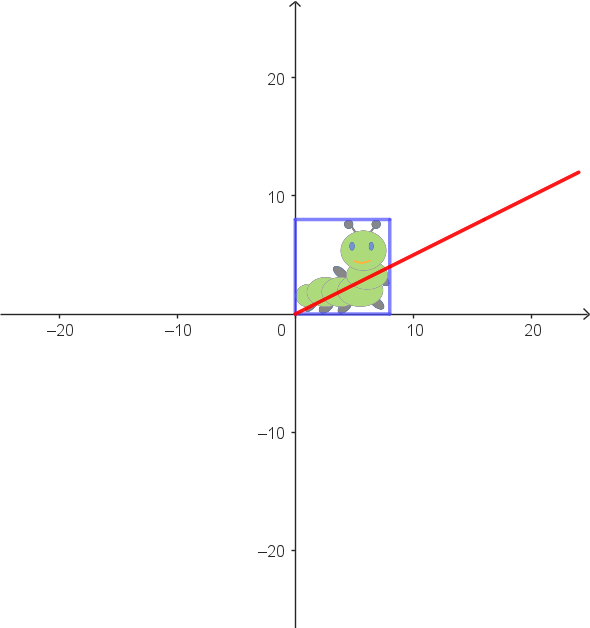
|
|
|
Zuordnungsbeispiele: $\alpha: \begin{pmatrix} 8 \\ 0 \end{pmatrix} \rightarrow \begin{pmatrix} 8 \\ 4 \end{pmatrix}$ $\alpha: \begin{pmatrix} 0 \\ 4 \end{pmatrix} \rightarrow \begin{pmatrix} 8 \\ 4 \end{pmatrix}$ |
Zuordnungsbeispiele: $\alpha^{-1}: \begin{pmatrix} 8 \\ 4 \end{pmatrix} \rightarrow ?$ |
|
Vektorgleichung als allgemeine Zuordnungsvorschrift: $\alpha: \begin{pmatrix} x_1' \\ x_2' \end{pmatrix} = \begin{pmatrix} 1 & 2 \\ 0.5 & 1 \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}$ |
Vektorgleichung als allgemeine Zuordnungsvorschrift: $\alpha^{-1}$ existiert nicht |
Aufgabe 1
Mache dich noch einmal mit den Zusammenhängen in den bereits bearbeiteten Beispielen vertraut.
Begriffe klären
Wir präzisieren zunächst die bereits (intuitiv) verwendeten Begriffe.
Umkehrabbildung
Eine geometrische Abbildung $\alpha$ ist umkehrbar genau dann, wenn sie unterschiedliche Vektoren (bzw. Punkte) jeweils auf unterschiedliche Bildvektoren (bzw. Bildpunkte) abbildet.
Die Umkehrbarabbildung $\alpha^{-1}$ zu einer vorgegebenen geometrischen Abbildung $\alpha$ kehrt die Zuordnungen der vorgegebenen Abbildung $\alpha$ alle um – sofern die Abbildung umkehrbar ist.
Das Zusammenspiel von Abbildung und Umkehrabbildung lässt sich auch so beschreiben: Wenn man zuerst die Abbildung $\alpha$ auf einen Vektor anwendet und anschließend die Umkehrabbildung $\alpha^{-1}$ auf den Bildvektor, dann erhält man wieder den Ausgangsvektor.
In Beispiel 1 sieht man das anhand ausgewählter Zuordnungen:
$\begin{pmatrix} 8 \\ 0 \end{pmatrix} \stackrel{\alpha}{\longrightarrow} \begin{pmatrix} 8 \\ 16 \end{pmatrix} \stackrel{\alpha^{-1}}{\longrightarrow} \begin{pmatrix} 8 \\ 0 \end{pmatrix}$
Die Verkettung von Abbildung und Umkehrabbildung muss also folgende Bedingung erfüllen:
$\alpha^{-1} \circ \alpha: \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} \rightarrow \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}$ bzw. $\alpha^{-1} \circ \alpha: \begin{pmatrix} x_1' \\ x_2' \end{pmatrix} = \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}$
Die Verkettung $\alpha^{-1} \circ \alpha$ von Abbildung und Umkehrabbildung ergibt die identische Abbildung, die jeden Vektor auf sich selbst abbildet.
Aufgabe 2
Verdeutliche die Begriffe und Zusammenhänge an den oben gezeigten Beispielen.
Zielsetzung
In den folgenden Abschnitte verallgemeinern wir die Ergebnisse aus dem letzten Kapitel zur Bestimmung von Umkehrabildungen.

