Zusammenfassung - Verkettung geometrischer Abbildungen

Die Grundidee

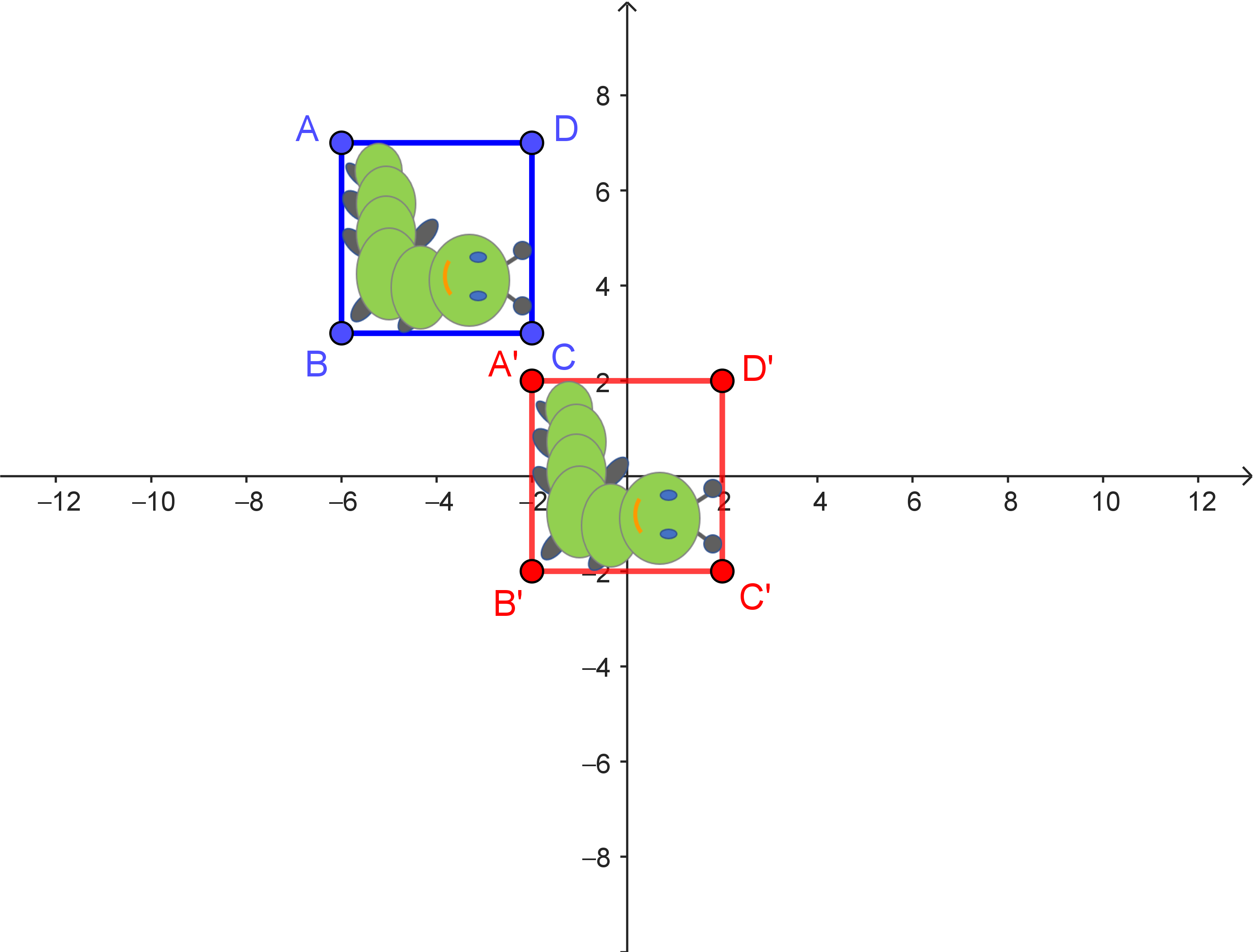
Ziel ist es, eine Drehung um $90°$ um das Drehzentrum $(-4|5)$ algebraisch zu beschreiben. Diese Abbildung kann man mit Hilfe von $3$ Teilabbildungen durchführen, die hintereinander ausgeführt werden. Das Hintereinanderausführen von Teilabbildungen nennt man auch Verketten von Abbildungen.

Teilabbildung 1	Teilabbildung 2	Teilabbildung 3
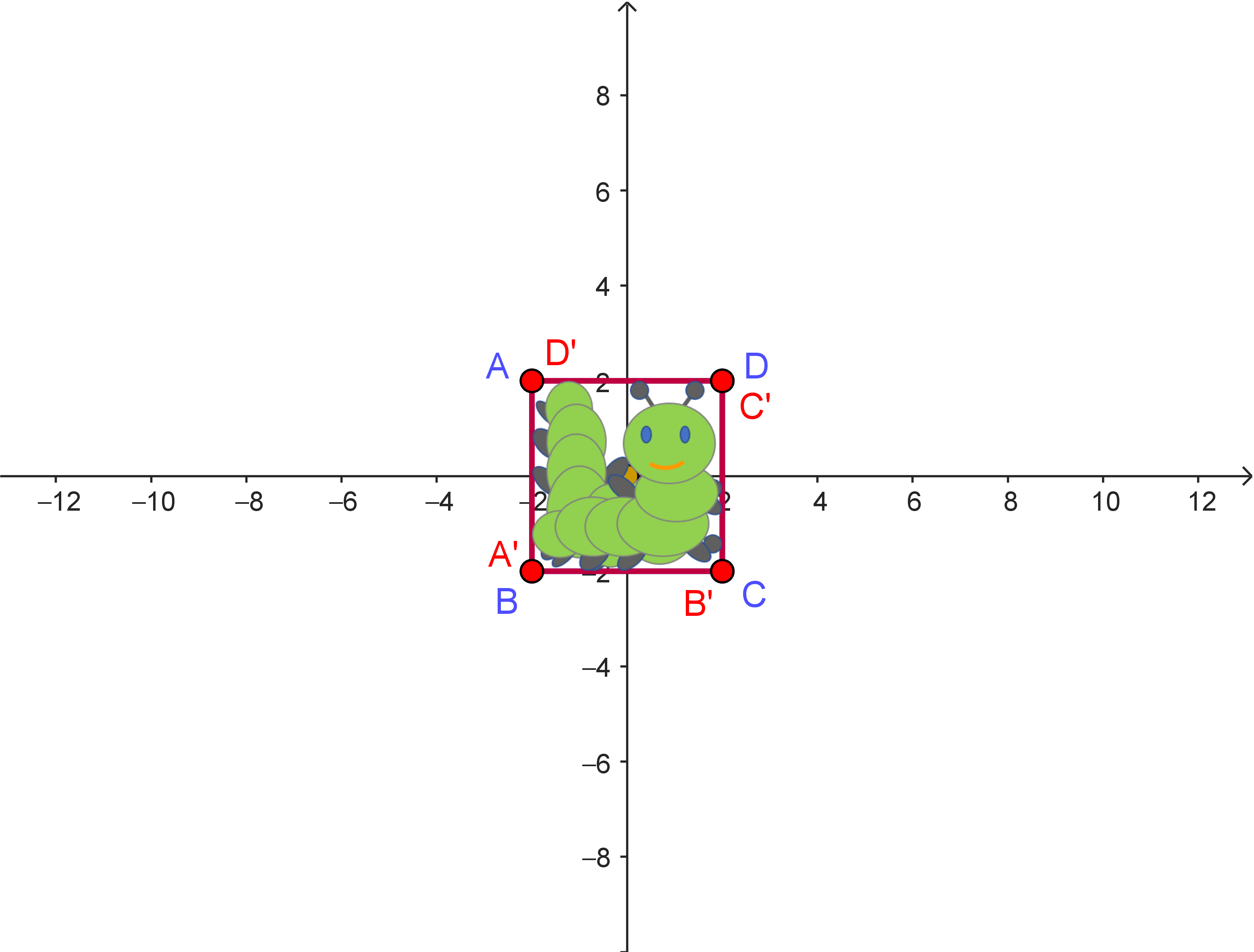
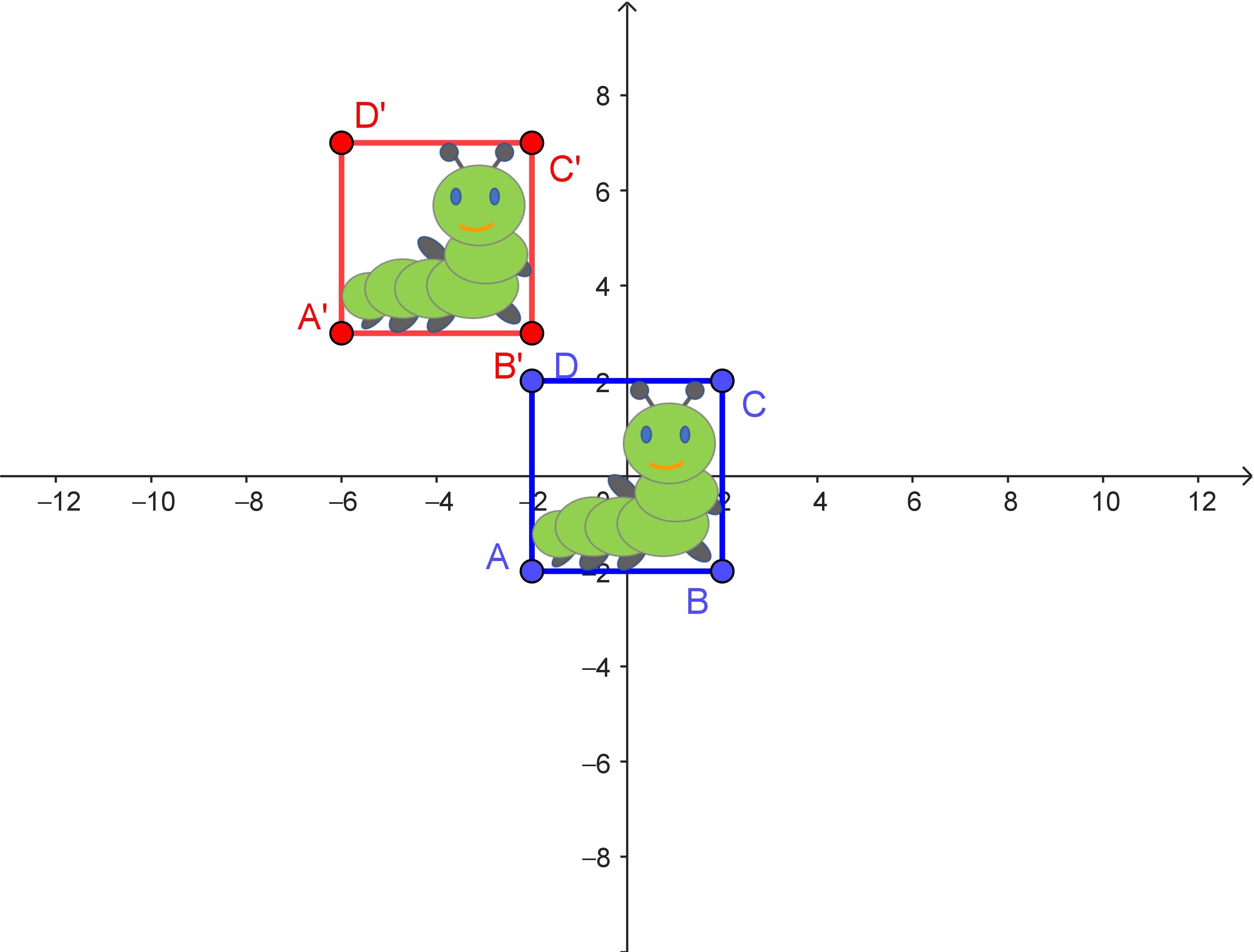
Verschiebung um $4$ nach rechts und $5$ nach unten	Drehung um $90°$ um den Ursprung	Verschiebung um $4$ nach links und $5$ nach oben
$\alpha: \begin{pmatrix} x_1' \\ x_2' \end{pmatrix} = \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} + \begin{pmatrix} 4 \\ -5 \end{pmatrix}$	$\beta: \begin{pmatrix} x_1' \\ x_2' \end{pmatrix} = \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}$	$\gamma: \begin{pmatrix} x_1' \\ x_2' \end{pmatrix} = \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} + \begin{pmatrix} -4 \\ 5 \end{pmatrix}$

In der Übersicht sind auch bereits die algebraischen Beschreibungen zu den Teilabbildungen aufgeführt. Beachte, dass wir hier die Bezeichnung $\alpha$, $\beta$ und $\gamma$ als Abkürzungen für die Teilabbildungen verwenden. Es fehlt noch die algebraische Beschreibung der Gesamtabbildung, die man durch eine Verkettung (bzw. durch Hintereinanderausführen) der Teilabbildungen erhält.

Verkettung der Teilabbildungen – am Beispiel

Verkettung der Teilabbildungen – allgemein

$\begin{array}{c} \begin{pmatrix} -6 \\ 7 \end{pmatrix} \\ \\ \downarrow \alpha\\ \\ \begin{pmatrix} -6 \\ 7 \end{pmatrix} + \begin{pmatrix} 4 \\ -5 \end{pmatrix} = \begin{pmatrix} -2 \\ 2 \end{pmatrix} \\ \\ \downarrow \beta \\ \\ \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} \cdot \left[ \begin{pmatrix} -6 \\ 7 \end{pmatrix} + \begin{pmatrix} 4 \\ -5 \end{pmatrix} \right] = \begin{pmatrix} -2 \\ -2 \end{pmatrix} \\ \\ \downarrow \gamma\\ \\ \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} \cdot \left[ \begin{pmatrix} -6 \\ 7 \end{pmatrix} + \begin{pmatrix} 4 \\ -5 \end{pmatrix} \right] + \begin{pmatrix} -4 \\ 5 \end{pmatrix} = \begin{pmatrix} -6 \\ 3 \end{pmatrix} \end{array}$

$\begin{array}{c} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} \\ \\ \downarrow \alpha\\ \\ \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} + \begin{pmatrix} 4 \\ -5 \end{pmatrix} \\ \\ \downarrow \beta \\ \\ \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} \cdot \left[ \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} + \begin{pmatrix} 4 \\ -5 \end{pmatrix} \right] \\ \\ \downarrow \gamma\\ \\ \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} \cdot \left[ \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} + \begin{pmatrix} 4 \\ -5 \end{pmatrix} \right] + \begin{pmatrix} -4 \\ 5 \end{pmatrix} \end{array}$

Die Verkettung von $\alpha$, $\beta$ und $\gamma$ bildet den Ausgangsvektor $\begin{pmatrix} -6 \\ 7 \end{pmatrix}$ auf den Bildvektor $\begin{pmatrix} -6 \\ 3 \end{pmatrix}$ ab:

$\begin{pmatrix} -6 \\ 7 \end{pmatrix} \stackrel{\alpha}{\longrightarrow} \stackrel{\beta}{\longrightarrow} \stackrel{\gamma}{\longrightarrow} \begin{pmatrix} -6 \\ 3 \end{pmatrix}$

Wenn man die übliche Klammerschreibweise für Abbildungen verwendet, dann kann man das auch so schreiben:

$\gamma \left( \beta \left( \alpha \left( \; \begin{pmatrix} -6 \\ 7 \end{pmatrix} \; \right) \right) \right) = \begin{pmatrix} -6 \\ 3 \end{pmatrix}$

Es wird also $\gamma$ nach $\beta$ nach $\alpha$ ausgeführt. Die Gesamtabbildung $\gamma$ nach $\beta$ nach $\alpha$ beschreibt man in der Form $\gamma \circ \beta \circ \alpha$. Es gilt also:

$\begin{pmatrix} -6 \\ 7 \end{pmatrix} \stackrel{\gamma \circ \beta \circ \alpha}{\longrightarrow} \begin{pmatrix} -6 \\ 3 \end{pmatrix}$

Aus der Übersicht oben entnimmt man, dass man die Abbildung $\gamma \circ \beta \circ \alpha$ algebraisch so beschreiben kann:

$\gamma \circ \beta \circ \alpha : \begin{pmatrix} x_1' \\ x_2' \end{pmatrix} = \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} \cdot \left[ \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} + \begin{pmatrix} 4 \\ -5 \end{pmatrix} \right] + \begin{pmatrix} -4 \\ 5 \end{pmatrix}$

Verkettung von Abbildungen

Wir legen die im Beispiel oben bereits verwendeten Begriffe und Symbole jetzt präzise fest.

Verkettung von linearen Abbildungen

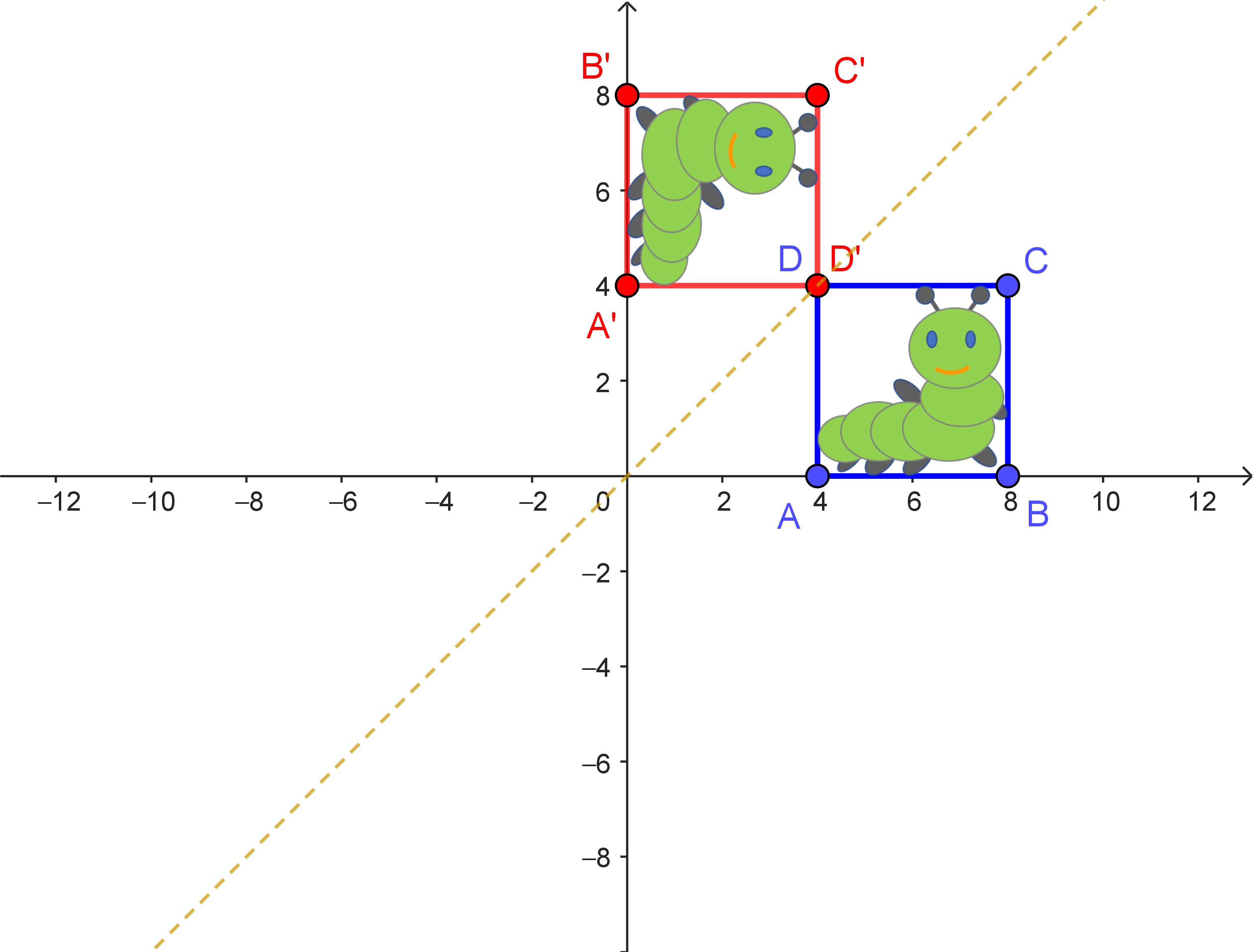
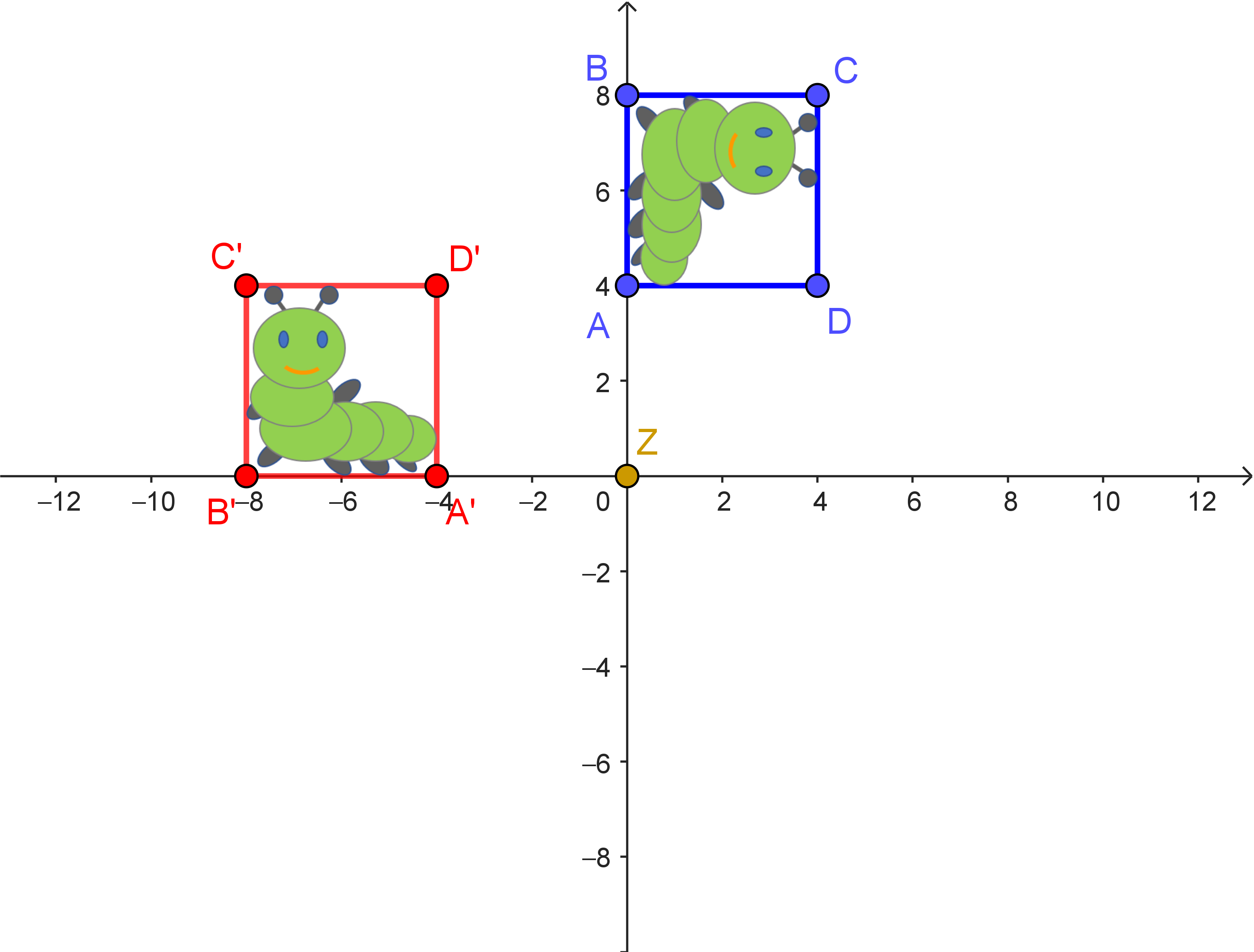
Wenn man die Verkettung $\beta \circ \alpha$: Drehung um $90°$ um den Ursprung nach Spiegelung an der 1. Winkelhalbierenden durchführt, dann sieht es so aus, als entspräche das einer Spiegelung an der $y$-Achse.

Teilabbildung 1	Teilabbildung 2	Vergleichsabbildung
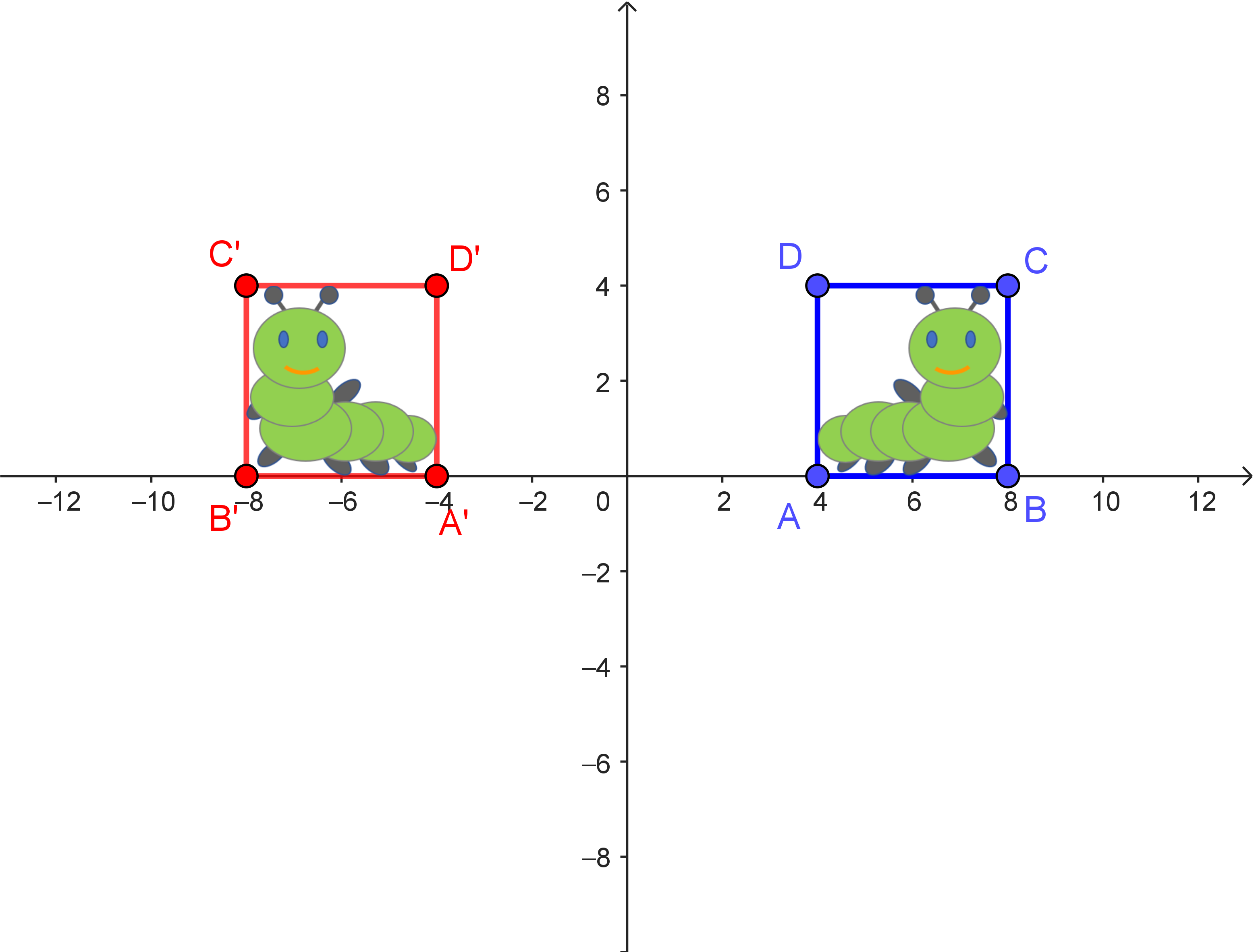
Spiegelung an der 1. Winkelhalbierenden	Drehung um $90°$ um den Ursprung	Spiegelung an der $y$-Achse
$\alpha: \begin{pmatrix} x_1' \\ x_2' \end{pmatrix} = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}$	$\beta: \begin{pmatrix} x_1' \\ x_2' \end{pmatrix} = \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}$	$\gamma: \begin{pmatrix} x_1' \\ x_2' \end{pmatrix} = \begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}$

Stimmt das auch – nicht nur für die im Bild gezeigte Figur? Das kann man algebraisch überprüfen. Hierzu nutzen wir die algebraischen Beschreibungen der beiden Teilabbildungen.

$\begin{pmatrix} x_1 \\ x_2 \end{pmatrix} \stackrel{\alpha}{\longrightarrow} \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} \stackrel{\beta}{\longrightarrow} \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} \cdot \left[\begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}\right]$

Mit dem Assoziativgesetz für die Matrixmultiplikation erhält man:

$\begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} \cdot \left[\begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}\right] = \left[\begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}\right] \cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = \begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}$

Es gilt also:

$\beta \circ \alpha: \begin{pmatrix} x_1' \\ x_2' \end{pmatrix} = \begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}$

Die Verkettung $\beta \circ \alpha$ entspricht somit genau einer Spiegelung an der $y$-Achse.

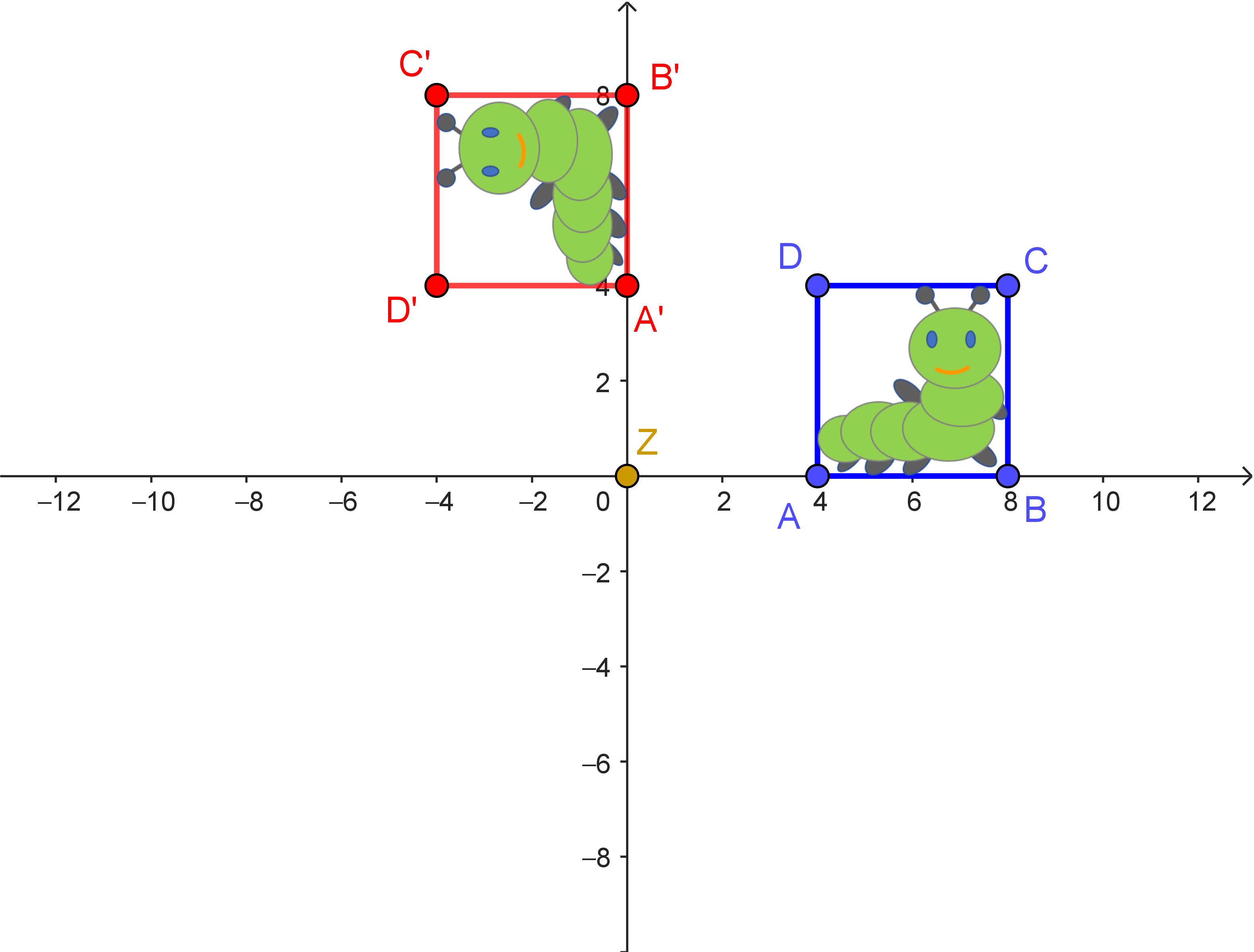
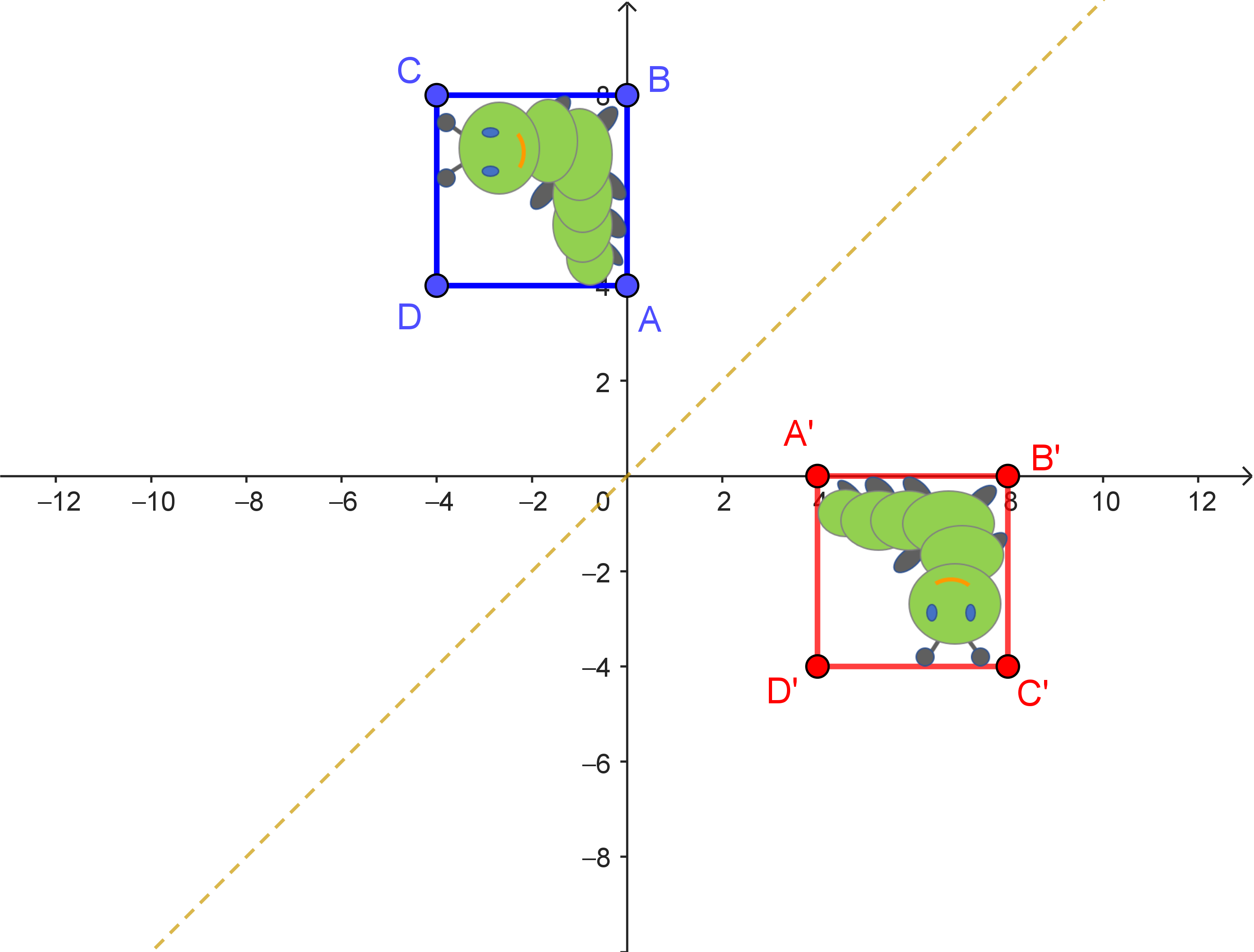
Analog kann man zeigen, dass die umgekehrte Verkettung $\alpha \circ \beta$ einer Spiegelung an der $x$-Achse entspricht.

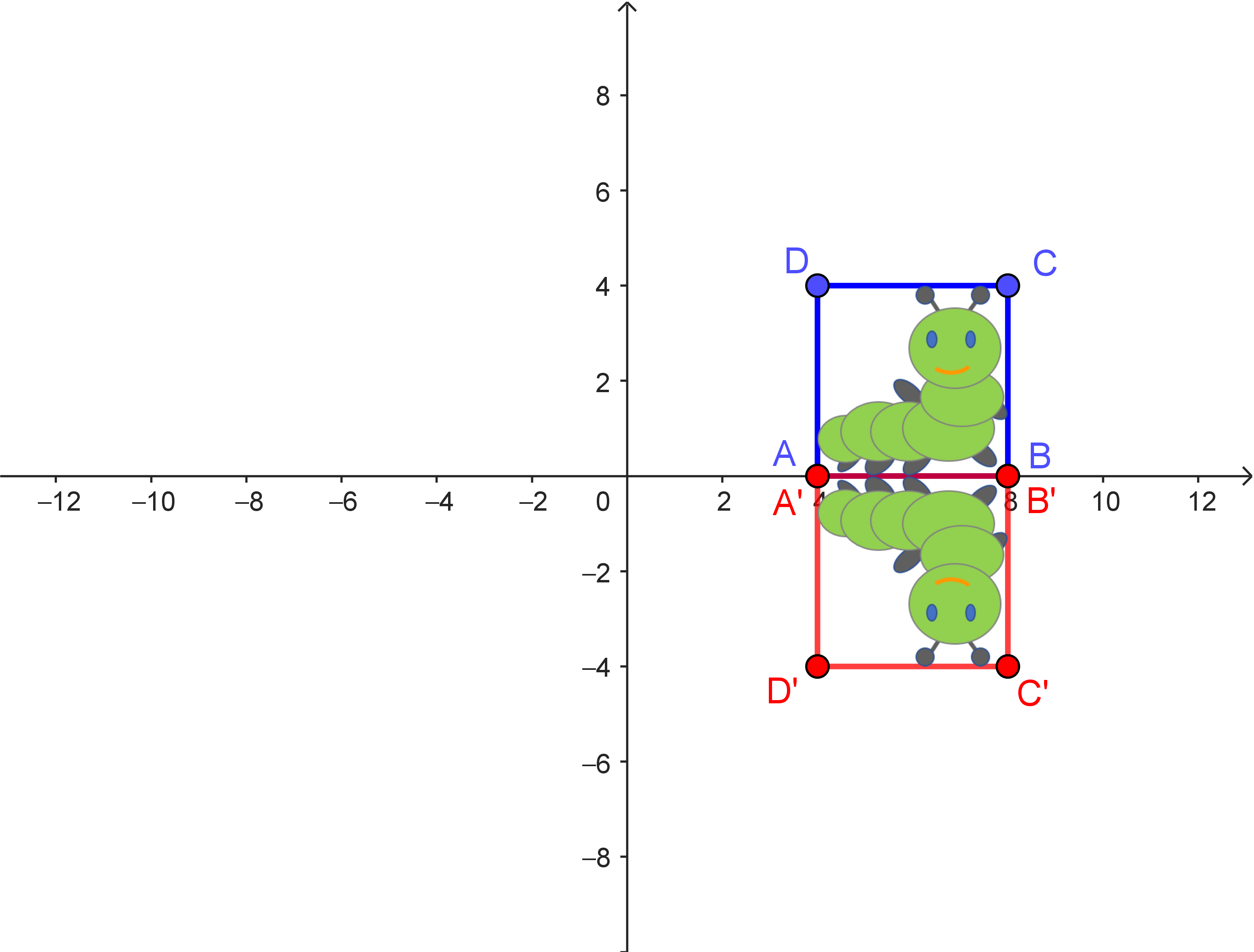
Teilabbildung 1	Teilabbildung 2	Vergleichsabbildung
Drehung um $90°$ um den Ursprung	Spiegelung an der 1. Winkelhalbierenden	Spiegelung an der $x$-Achse
$\beta: \begin{pmatrix} x_1' \\ x_2' \end{pmatrix} = \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}$	$\alpha: \begin{pmatrix} x_1' \\ x_2' \end{pmatrix} = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}$	$\gamma: \begin{pmatrix} x_1' \\ x_2' \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}$

Die Betrachtungen lassen sich verallgemeinern:

Beachte: Die Verkettung von (linearen) Abbildungen ist nicht kommutativ.

Verkettung von affinen Abbildungen

Wie wirkt sich eine Verkettung bei affinen Abbildungen aus? In dr folgenden Übersicht wird das an einem einfachen Beispiel demonstriert.

Teilabbildung 1	Teilabbildung 2	Vergleichsabbildung
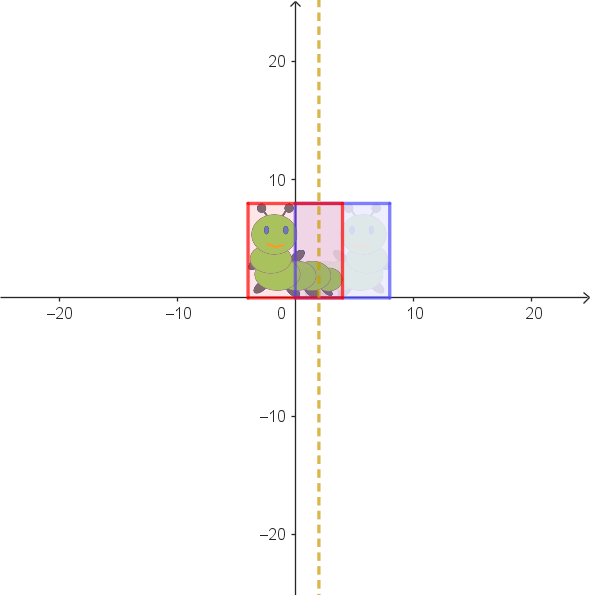
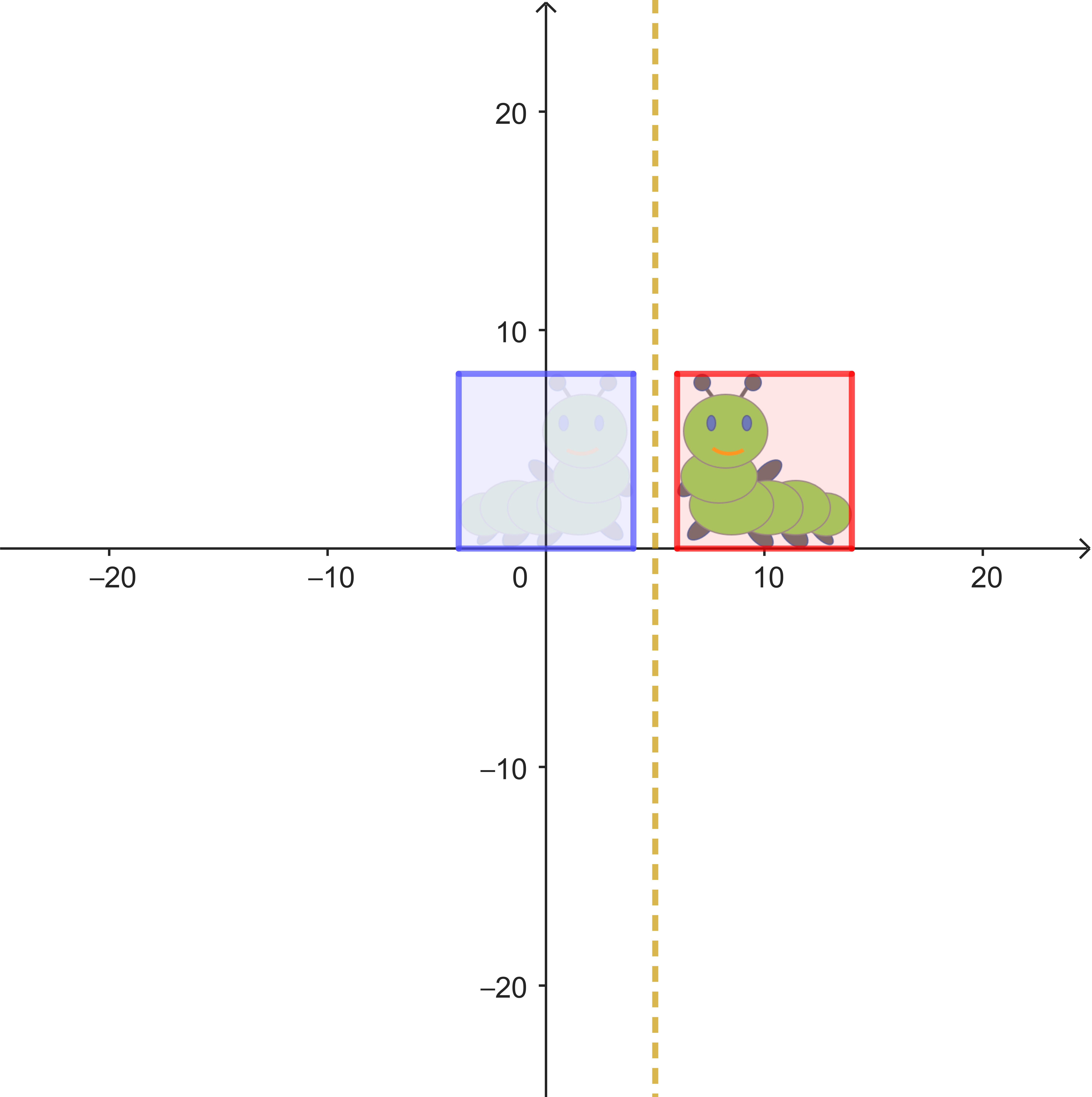
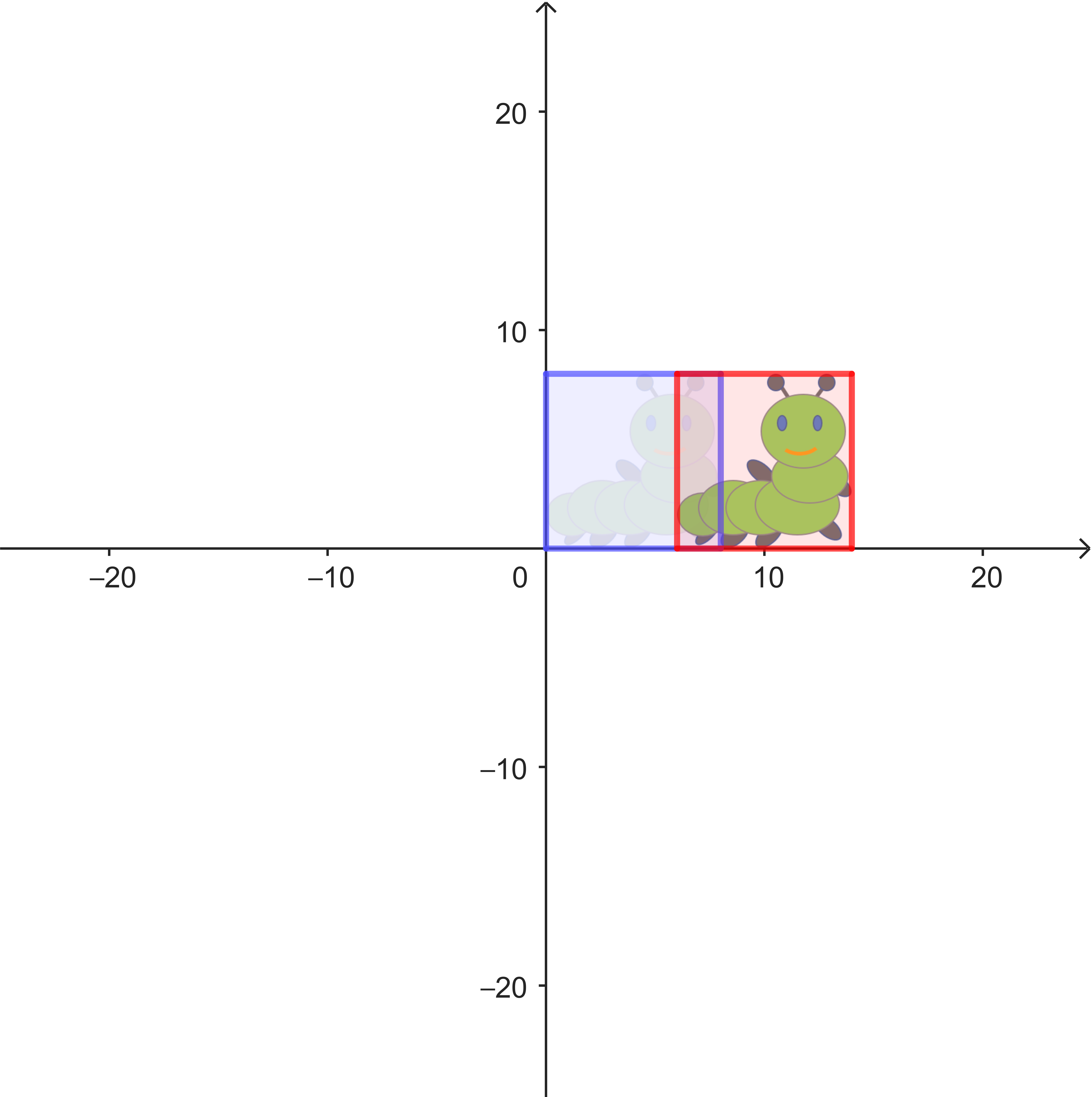
Spiegelung an der Geraden $x = 2$	Spiegelung an der Geraden $x = 5$	Verschiebung um $6$ nach rechts
$\alpha: \begin{pmatrix} x_1' \\ x_2' \end{pmatrix} = \begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} + \begin{pmatrix} 4 \\ 0 \end{pmatrix}$	$\beta: \begin{pmatrix} x_1' \\ x_2' \end{pmatrix} = \begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} + \begin{pmatrix} 10 \\ 0 \end{pmatrix}$	$\gamma: \begin{pmatrix} x_1' \\ x_2' \end{pmatrix} = \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} + \begin{pmatrix} 6 \\ 0 \end{pmatrix}$ bzw. $\gamma: \begin{pmatrix} x_1' \\ x_2' \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} + \begin{pmatrix} 6 \\ 0 \end{pmatrix}$

Es sieht so aus, als ob die Verkettung von zwei Spiegelungen hier zu einer Verschiebung führt. Das lässt sich recherisch überprüfen.

$\begin{pmatrix} x_1 \\ x_2 \end{pmatrix} \stackrel{\alpha}{\longrightarrow} \begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} + \begin{pmatrix} 4 \\ 0 \end{pmatrix} \stackrel{\beta}{\longrightarrow} \begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix} \cdot \left[\begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} + \begin{pmatrix} 4 \\ 0 \end{pmatrix}\right] + \begin{pmatrix} 10 \\ 0 \end{pmatrix}$

Mit dem Distributivgesetz und dem Assoziativgesetz für die Matrixmultiplikation erhält man:

$\begin{array}{l} \begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix} \cdot \left[\begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} + \begin{pmatrix} 4 \\ 0 \end{pmatrix}\right] + \begin{pmatrix} 10 \\ 0 \end{pmatrix} = \\ \begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix} \cdot \left[\begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}\right] + \begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 4 \\ 0 \end{pmatrix} + \begin{pmatrix} 10 \\ 0 \end{pmatrix} = \\ \left[\begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix}\right] \cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} + \begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 4 \\ 0 \end{pmatrix} + \begin{pmatrix} 10 \\ 0 \end{pmatrix} = \\ \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} + \begin{pmatrix} -4 \\ 0 \end{pmatrix} + \begin{pmatrix} 10 \\ 0 \end{pmatrix} = \\ \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} + \begin{pmatrix} 6 \\ 0 \end{pmatrix} = \\ \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} + \begin{pmatrix} 6 \\ 0 \end{pmatrix} \end{array}$

Es gilt also:

$\beta \circ \alpha: \begin{pmatrix} x_1' \\ x_2' \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} + \begin{pmatrix} 6 \\ 0 \end{pmatrix} = \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} + \begin{pmatrix} 6 \\ 0 \end{pmatrix}$

Die Verkettung $\beta \circ \alpha$ entspricht somit genau einer Verschiebung in $x$-Richtung.

Auch hier lassen sich die Betrachtungen verallgemeinern:

Beachte: Die Verkettung von (affinen) Abbildungen ist nicht kommutativ.