o-mathe | Die Umkehrregel » Zusammenfassung

Zusammenfassung – Die Umkehrregel

Das Problem

Wir betrachten die folgende Ausgangssituation. Die Umkehrfunktion $f^{-1}$ zu einer Ausgangsfunktion $f$ soll abgeleitet werden.

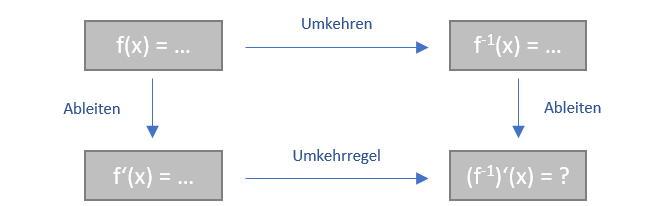
Man kann versuchen, die Ableitungsfunktion direkt (mit Hilfe der Definition der Ableitung) abzuleiten. Günstiger wäre es, wenn man die Ableitung der Ausgangsfunktion hierzu nutzen könnte. Hierfür benötigt man eine geeeignete Ableitungsregel, die es ermöglicht, aus der Ableitung $f'$ der Ausgangsfunktion die Ableitung $(f^{-1})'$ der zugehörigen Umkehrfunktion zu bestimmen.

Herleitung einer Ableitungsregel für Umkehrfunktionen

Wir gehen bei der Herleitung einer Ableitungsregel für Umkehrfunktionen deduktiv vor. Das heißt, wir greifen auf bereits bekannte Zusammenhänge zurück und nutzen sie, um die Ableitungsregel zu erschließen. Das folgende Applet verdeutlicht diese Zusammenhänge.

Zum Herunterladen: umkehrregel1.ggb

Mache dir anhand des Applets die folgenden Zusammenhänge klar.

Gegeben ist eine umkehrbare Funktion $f$ und ihre Umkehrfunktion $f^{-1}$. Im Applet wird diese Ausgangssituation am Beispiel der Quadratfunktion und der Wurzelfunktion als Umkehrfunktion verdeutlicht. Der Graph der Ausgangsfunktion ist dabei blau, der Graph der zugehörigen Umkehrfunktion grün dargestellt.
Die beiden Graphen von $f$ und $f^{-1}$ liegen spiegelbildlich zur Winkelhalbierenden $y = x$. Man erhält Graph $f^{-1}$, indem man Graph $f$ an dieser Winkelhalbierenden spiegelt und umgekehrt.
Betrachte eine beliebige Stelle $x$ aus der Definitionsmenge der Umkehrfunktion $f^{-1}$. Im Applet ist die Stelle $x$ mit einem roten Punkt auf der $x$-Achse markiert. Man kann diesen roten Punkt auf der $x$-Achse hin und her bewegen und so die Stelle $x$ variieren.
Der Punkt $P(x|y)$ markiert den zu $x$ gehörenden Punkt auf dem Graph der Umkehrfunktion $f^{-1}$. Es gilt also $y = f^{-1}(x)$.
Die Ableitung $(f^{-1})'(x)$ beschreibt die Steigung von Graph $f^{-1}$ an der Stelle $x$ bzw. die Steigung der Tangente an Graph $f^{-1}$ im Punkt $P$. Im Applet wird diese Tangente mit $t_{f^{-1}}$ bezeichnet und mit einer grün gepunkteten Geraden angezeigt.
Zum Punkt $P(x|y)$ auf Graph $f^{-1}$ gibt es einen spiegelbildlich angeordneten Punkt $Q(y|x)$ auf Graph $f$. Beachte, dass man die Koordinaten von $Q$ durch Vertauschen der Koordinaten von $P$ erhält.
Die Ableitung $f'(y)$ beschreibt die Steigung von Graph $f$ an der Stelle $y$ bzw. die Steigung der Tangente an Graph $f$ im Punkt $Q$. Im Applet wird diese Tangente mit $t_{f}$ bezeichnet und mit einer blau gepunkteten Geraden angezeigt.
Die Tangenten $t_{f}$ und $t_{f^{-1}}$ liegen – genau wie Graph $f$ und Graph $f^{-1}$ – spiegelbildich zur Winkelhalbierenden $y = x$. Ebenfalls spiegelbildlich dargestellt sind die beiden Steigungsdreiecke an den Tangenten $t_{f}$ und $t_{f^{-1}}$.
Das Spiegeln vertauscht die Rollen der Schrittweite und der Änderung in den Steigungsdreiecken. Die Schrittweite im grün dargestellten Steigungsdreieck entspricht der Änderung im blau dargestellten Steigungsdreieck. Ebenso entspricht die Änderung im grün dargestellten Steigungsdreieck der Schrittweite im blau dargestellten Steigungsdreieck. Hieraus folgt, dass $m_P = \displaystyle{\frac{1}{m_Q}}$ gilt.

Mit diesen Zusammenhängen kann man jetzt die folgende Regel zum Ableiten von $f^{-1}$ erschließen:

$(f^{-1})'(x) = m_{P} = \displaystyle{\frac{1}{m_Q}} = \displaystyle{\frac{1}{f'(y)}} = \displaystyle{\frac{1}{f'(f^{-1}(x))}}$

Die Ableitung der Umkehrfunktion erhält man also aus der Ableitung der Ausgangsfunktion am Funktionswert der Umkehrfunktion. Die Herleitung dieser Regel ist an einige Voraussetzung geknüpft, die wir im folgenden Satz der Vollständigkeit halber auflisten.

Umkehrregel

Betrachte eine Funktion $f$, die umkehrbar ist und die an einer Stelle $x$ differenzierbar ist. Wenn $f'(f^{-1}(x)) \neq 0$ und wenn zusätzlich $f^{-1}$ an der Stelle $x$ stetig ist, dann gilt:

$(f^{-1})'(x) = \displaystyle{\frac{1}{f'(f^{-1}(x))}}$

Beispiel 1

Betrachte die Funktion $f$ mit $f(x) = x^2$ und der Definitionsmenge $0 \lt x \lt \infty$. Für diese Funktion gilt:

$f'(x) = 2x$
$f^{-1}(x) = \sqrt{x}$

Mit der Umkehrregel erhält man:

$(f^{-1})'(x) = \displaystyle{\frac{1}{f'(f^{-1}(x))}} = \displaystyle{\frac{1}{2\sqrt{x}}}$

Beachte: Die Umkehrregel liefert dieselbe Ableitung wie die verallgemeinerte Potenzregel, wenn man sie auf $f^{-1}(x) = \sqrt{x} = x^{\frac{1}{2}}$ anwendet:

$\displaystyle{(f^{-1})'(x) = \frac{1}{2} \cdot x^{-\frac{1}{2}} = \frac{1}{2 x^\frac{1}{2}} = \frac{1}{2 \sqrt{x}}}$

Beispiel 2

Betrachte die Funktion $f$ mit $f(x) = e^x$. Für diese Funktion gilt:

$f'(x) = e^{x}$
$f^{-1}(x) = \ln(x)$

Mit der Umkehrregel erhält man:

$(f^{-1})'(x) = \displaystyle{\frac{1}{f'(f^{-1}(x))}} = \displaystyle{\frac{1}{e^{\ln(x)}}} = \displaystyle{\frac{1}{x}}$

Herleitung der Umkehrregel mit der Kettenregel

Für eine Funktion $f$ und ihre Umkehrfunktion $f^{-1}$ gilt $f(f^{-1}(x)) = x$, da die Umkehrfunktion die Zuordnungen der Ausgangsfunktion rückgängig macht.

$f \circ f^{-1}: x \stackrel{f^{-1}}{\rightarrow} y = f^{-1}(x) \stackrel{f}{\rightarrow} x = f(f^{-1}(x))$

Verkürzt kann man diesen Zusammenhang mit der Identitätsfunktion $i$ mit $i(x) = x$ so beschreiben:

$f \circ f^{-1} = i$

Wir bilden die Ableitungen:

$(f \circ f^{-1})'(x) = f'(f^{-1}(x)) \cdot (f^{-1})'(x)$ (mit der Kettenregel)
$i'(x) = 1$ (mit der Potenzregel)

Es gilt also $f'(f^{-1}(x)) \cdot (f^{-1})'(x) = 1$. Durch Umformen erhält man die Formel zur Umkehrregel: