Vertiefung
Zur Orientierung
Warum ist es günstig, wenn man Funktionen rechnerisch kombinieren kann? Das soll in diesem Abschnitt an einem einfachen Beispiel aufgezeigt werden.
Funktionen rechnerisch kombinieren
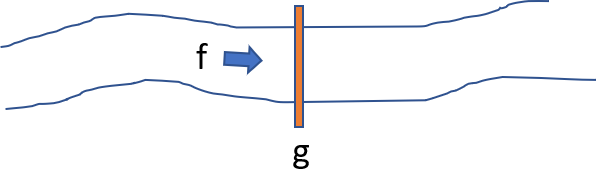
Wir betrachten noch einmal eine Situation, bei der die Durchflussrate eines Baches kontrolliert wird. Zur Regelung bei Starkregen ist ein Tor vorgesehen, das bei Gefahr geschlossen werden kann und so die Durchflussrate reduzieren kann.
Aufgabe 1
Im folgenden Applet sind wird die Situation mit Hilfe von Funktionen modelliert.
- Die Funktion $f$ beschreibt die Durchflussrate des Baches. Im Applet wird ein quadratischer Anstieg der Durchflussrate simuliert. Beachte, dass wir nur an den Funktionswerten für nicht-negative $x$-Werte interessiert sind.
- Mit der Funktion $g$ wird die Regelung des Tores modelliert. Wenn $g(x) = 1$ gilt, dann wird zum Zeitpunkt $x$ die gesamte Wassermenge durchgelassen – das Tor ist also offen. Wenn $g(x) = 0$ gilt, dann soll das Tor zum Zeitpunkt $x$ geschlossen sein.
-
Wir betrachten die Situation nur in dem Zeitintervall, in dem das Tor von
offen
hin zugeschlossen
geregelt wird.
Noch nicht richtig modelliert ist das Rechenzeichen, das zur Kombination der beiden Funktionen benutzt werden soll. Korrigiere das Rechenzeichen und beschreibe, wie sich die Kombination der beiden Funktionen hier auswirkt.
Zum Herunterladen: funktionenrechner3.ggb
Aufgabe 2
Begründe, warum es günstig ist, den gesamten Vorgang mit zwei Funktionen zu modellieren? Betrachte hierzu Möglichkeiten zur Variation des simulierten Vorgangs.

