Zusammenfassung – Verkettung von Funktionen
Die Ausgangssituation
Du hast beim letzten Besuch in deinem Liebingsladen einen Gutschein über 5€ erhalten. Den willst du jetzt einlösen. Im Laden angekommen stellst du erfreut fest, dass es gerade auch noch eine Rabattaktion gibt: 10% Nachlass auf alle Artikel. Du suchst dir im Laden etwas aus und gehst zur Kasse.
An der Kasse:
Kein Problem, unsere Kasse ist so programmiert, dass sie Gutscheine und Rabattaktionen berücksichtigen Kombination –
und das sogar auf zwei verschiedene Weisen.
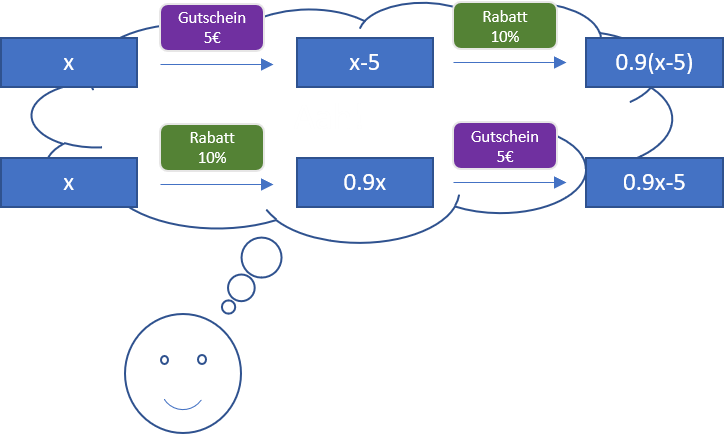
Die Berechnungen in der Kasse werden mit Hilfe von Funktionen durchgeführt:
- Eine Funktion $v$ beschreibt, wie man einen Gutschein von $5$€ verrechnet: $u(x) = x - 5$.
- Eine Funktion $u$ beschreibt, wie man einen Rabatt von $10$% gewährt: $u(x) = 0.9 \cdot x$.
Das folgende Applet zeigt, wie man die Preisberechnungen im Fall erst den Gutschein einlösen und dann den Rabatt gewähren
mit Hilfe von Funktionen modelliert.
Zum Herunterladen: verkettung1.ggb
Hier werden zwei Funktionen hintereinander ausgeführt. Man sagt auch, sie werden verkettet.
Präzierung der Verkettung von Funktionen
Betrachte zwei Funktionen $u$ und $v$, die hintereinander ausgeführt werden: erst die Funktion $v$, dann die Funktion $u$
bzw. $u$ wird nach $v$ ausgeführt
.
$x \stackrel{v}{\rightarrow} v(x) \stackrel{u}{\rightarrow} u(v(x))$
Hierdurch entsteht eine neue Funktion $f$ mit $f(x) = u(v(x))$.
$x \stackrel{f}{\rightarrow} u(v(x))$
Verkettung von Funktionen
Die Verknüpfung der beiden Funktionen $u$ und $v$ durch Hintereinanderausführen beschreibt man mit dem Verknüpfungszeichen $\circ$:
$f = u \circ v$ mit $f(x) = u(v(x))$
Gelesen wird $f = u \circ v$ so: $f$ ist gleich $u$ nach $v$
.
Diese Verknüpfung von Funktionen nennt man Verkettung (bzw. Komposition) von Funktionen.
Wenn $f = u \circ v$ bzw. $f(x) = u(v(x))$, dann nennt man $v$ innere Funktion und $u$ äußere Funktion.
Beachte: Wenn $f = u \circ v$, dann ist die Funktion $f$ nur für solche $x$-Werte definiert, für die $x$ in der Definitionsmenge von $v$ liegt und für die zusätzlich $v(x)$ in der Definitionsmenge von $u$ liegt.
Die beiden Beispiele verdeutlichen die Verkettung von Funktionen.
Beispiel 1
Gegeben sind zwei Funktionen:
- $v(x) = x-1$ (innere Funktion)
- $u(x) = \sqrt{x}$ (äußere Funktion)
Die Verkettung $u \circ v$ ergibt die Funktion $f$ mit $f(x) = u(v(x)) = \sqrt{x-1}$.
Beachte: $f$ ist nur für reellen Zahlen definiert, die größer oder gleich $1$ sind.
Beispiel 2
Gegeben sind zwei Funktionen:
- $v(x) = \sqrt{x}$ (innere Funktion)
- $u(x) = x - 1$ (äußere Funktion)
Die Verkettung $u \circ v$ ergibt die Funktion $f$ mit $f(x) = u(v(x)) = \sqrt{x} - 1$.
Beachte: $f$ ist nur für reellen Zahlen definiert, die größer oder gleich $0$ sind.

